-
Notifications
You must be signed in to change notification settings - Fork 0
UD series user interface
At this page we will be concentrated to the end-user's aims of series usage.
Now we determine in Function expansions and series that there exists many kind of series in mathematics. And that we must distinguish them from asymptotic expansions. (This situation was raised due to the historical development way of various CAS'es and remains f.e. in Sage and Wolfram Mathematica)
To be more extendable CAS in future the problems and use-cases will be considered for ideal CAS. Even when some of the problems will be not easy for realization or deserving for separated mathematical research. (The example of those problems is to find symbolic function knowing only coefficients of series.)
There is no doubts now that for efficient processing some object and classes will be needed and considered. End-user must know about them in minimal mode, only necessary for concrete task. But if task is complex then knowledge of them for user will be necessary extended too.
But we will not be concentrated to concrete algorithms or precise realizations, however we will take into consideration their basic shapes.
After discussion about this material we will be able to turn to the concrete plan of implementations: which issues can be isolated or how related, priority of them, how they are related with current situation, and so on.
Remark:
All of the name-tokens below are rough, also all code examples below are imaginary as desired or as variants offered.
They must be discussed further. Suggestions are needed too.
Main task for user is to obtain series.
Example:
>>> sin(x).series(x)
x + x**3/6 + x**5/120 + ...
Sometime more convenient to obtain asymptotic expansion for some expression or function:
>>> sin(x).expansion(x)
x + x**3/6 + x**5/120 + O(x**6)
Both .series(x) and .expansion(x) methods tells to user about terms and both methods cope with the main task.
Then he can try to manipulate with them thinking that they are some expressions. But it is unreasonably to operate for series only with a few first terms "x + x**3/6 + x**5/120" as ordinary polynomial (except on case of user want to do indeed and understand it) - series is infinite, so final result may be incorrect.
More sense to operate with expansion with Big-O notation:
>>> sin(x).expansion(x)
x + x**3/6 + x**5/120 + O(x**6)
>>> sin(x).expansion(x) + cos(x).expansion(x)
1 + x - x**2/2 - x**3/6 + x**4/24 + x**5/120 + O(x**6)
>>> cos(x).expansion(x)**2
1 - x**2 + x**4/3 + O(x**6)
Big-O signals to user what precision is and to do not forget terms of orders. Also it help for operations: eats high order terms which is not needed for user:
>>> cos(x).expansion(x)**2 + 1 + x + x**6 + 777*x**7 + x**8
2 + x - x**2 + x**4/3 + O(x**6)
This is the main historical motive why .series() method yield in many CAS'es expansion indeed: it is more convenient for user, prevalent task, and it was enough to implement O() behaviour to begin manipulate with them as ordinary expressions.
But we will be distinguish these objects, especially if there exists operations with series too if we consider them as the formal series:
>>> sin(x).series(x) + cos(x).series(x)
1 + x - x**2/2 - x**3/6 + x**4/24 + x**5/120 + ...
>>> cos(x).series(x)**2 + 1 + x + x**6 + 777*x**7 + x**8
2 + x - x**2 + x**4/3 + ...
It seems that there is no difference between the last result and the above analog result for .expansion(x) except the trailers "..." and "O()".
But the difference is that the last result continue remembering about "x**6 + 777*x**7 + x**8" terms.
>>> _.show(n=8)
2 + x - x**2 + x**4/3 + 43*x**6/45 + 777*x**7 + ...
One can wonder that it seems that sympy expression must secretly keep in mind the infinite number of terms. Is it really possible? Yes, it is possible in many cases.
User in above examples can do not suspect of internal representation of series. But really .series() method yield the expression of special type.
>>> s = sin(x).series(x)
>>> type(s)
<class 'sympy.series.PowerSeries'>
>>> a = sin(x).expansion(x)
>>> type(a)
sin(x).series(x)
<class 'sympy.series.PowerSeriesExpansion'>
Examples of operations for summation, multiplications which was described in previous section also are maintained by this classes.
These classes track some info about:
>>> s.expression
sin(x)
>>> s.variable
x
>>> s.coefficients(n=3)
[0, 1, 0, 1/6]
>>> a.precision
6
Have some methods for transformations.
Transformation of series to asymptotic expansion:
>>> s.to_expansion(n=6)
x - x**3/6 + x**5/120 + O(x**6)
Transformation of series to polynomial:
>>> s.to_polynomial(n=6)
Poly(x - x**3/6 + x**5/120, x, domain='ZZ')
Transformation of asymptotic expansion to polynomial:
>>> a.truncate() | a.removeO() | a.to_polynomial()
Poly(x - x**3/6 + x**5/120, x, domain='ZZ')
Transformation of asymptotic expansion object to ordinary sympy expression (but with Big-O):
>>> a.to_normal()
x - x**3/6 + x**5/120 + O(x**6)
>>> type(_)
<class 'sympy.core.add.Add'>
Representation variants:
>>> s.as_sum()
Sum(x**(n)/n! - x**(n+2)/(n+2)!, (n=1, 5, 9 ...))
Some properties:
>>> s.is_periodical()
False
>>> s.is_finite()
False
>>> s.to_taylor().coefficients(n=8)
[0, 1, 0, -1, 0, 1, 0, -1]
>>> s.to_taylor().is_periodical()
True
>>> s.to_taylor().period()
4
>>> s.to_taylor().sequence
Sequence(periodical=True, [0, 1, 0, -1])
Some analytic:
- isAnalytical
- hasLaurentSeries
- hasTaylorSeries
By matter:
- Series - infinte number of powers
- Expansion - finite number of powers, with O
- Polynome - finite number of powers
By range:
- non negative powers (infinite or finite) (PowerSeries, TaylorSeries)
- finite negative and (infinite or finite) positive powers (LaurentSeries)
- infinite negative and (infinite or finite) positive power (ClassicalLaurentSeries)
By internal representation:
- coefficients near x^k (PowerSeries, GeneratingFunction)
- coefficients near x^k/k! (TaylorSeries, GeneratingFunctionExponential)
- coefficients near some expression f.e. (x*log x)^k powers.
- coefficients near x^k and multiplpication of series by some expression
Image:
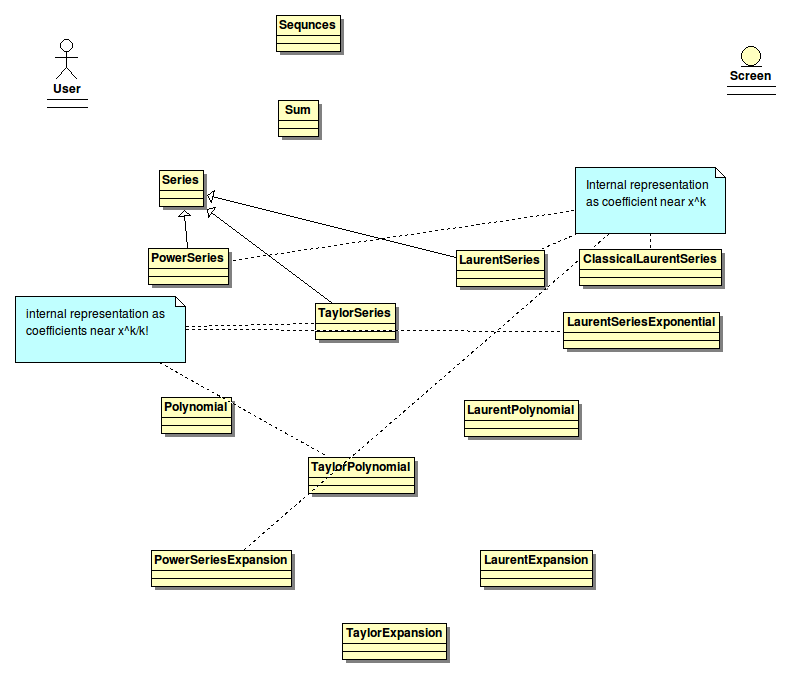

Power Series and Taylor Series, internal difference of them.
One difference is internal representation: that PowerSeries track coefficients near ( x^k ) terms, but TaylorSeries track coefficients near ( \frac{x^k}{n!} ) ones.
>>> ps = sin(x).series(kind="power")
>>> ps
x + x**3/6 + x**5/120 + ...
>>> ps.coefficients(n=5)
[1, 0, 1/6, 0, 1/120]
>>> type(ps)
<class 'sympy.series.PowerSeries'>
>>> ts = sin(x).series(kind="taylor")
>>> ts
x + x**3/6 + x**5/120 + ...
>>> ts.coefficients(n=5)
[1, 0, 1, 0, 1]
>>> type(ts)
<class 'sympy.series.TaylorSeries'>
Another difference is meaning: that TaylorSeries is defined as series from some function, while PowerSeries can be exists itself.
>>> ts.sourceFunction
sin(x)
>>> ps.sourceFunction
None
>>> ps == ts
???
The option (kind="taylor") more convenient and can be default.
Laurent
>>> s = (sin(x)/x**4).series(x)
>>> s
x**(-3) - 1/(6*x) + x/120 - x**3/5040 + x**5/362880 + ...
>>> type(s)
<class 'sympy.series.FormalLaurentSeries'>
>>> s.principalPart()
x**(-3) - 1/(6*x)
>>> (sin(x)/x**4).series(x, kind="taylor")
SeriesError:
ClassicalLaurent (infinite only negative powers)
>>> s = (exp(1/x)).series(x, oo)
>>> s
1 + 1/x + 1/(2*x**2) + 1/(6*x**3) + 1/(24*x**4) + 1/(120*x**5) + ...
>>> type(s)
<class 'sympy.series.ClassicalLaurentSeries'>
>>> s.x0 | s.point
oo
>>> s.principalPart().is_finite
False
>>> s.positivePart().is_finite
True
ClassicalLaurent infinite negative end positive powers: >>> s = (exp(x) + exp(1/x)).series(x) ... 1/(6x**3) + 1/(2x2) + 1/x + 1 + x + x2/2 + x**3/6 + ...
Multiplication is not allowed in this case.
>>> s*s
SeriesError: "Multiplication is not allowed"
In this case may be an annulus must be token into consideration. An *annulus* it is the area between two concentric circles
- Along with others specific methods to obtain specific series (Taylor, Laurent) a method to obtain series as a single procedure needs too - user may do not know what kind of series he have to obtain. This method plays a role of distribution job and is related with analyze job (isAnalytical, hasLaurentSeries and so on). Also this method can be used for limits processing implementation.
For expansion the same too.
through formula (finite or infinite sequence):
>>> Sequence((1, oo), k, 1/k)
[1, 1/2, 1/3, ...]
by recurrent formula or with the help of .rsolve() (finite or infinite sequence)
>>> Sequence((1, oo), rsolve(a(0)=1, a(i+1) = a(i) + 1 ) (see rsolve interface)
[1, 2, 3, 4, ...]
through periodical list (finite or infinite sequence)
>>> Sequence((0, oo), [1, 2, 3, 4], periodical=True)
[1, 2, 3, 4, 1, 2, 3, 4, ...]
through list (only finite sequence)
>>> Sequence((1, 4), [1, 2, 3, 4])
[1, 2, 3, 4]
through sequences (or like sequences constructor)
>>> s = TaylorSeries(x, sequence = Sequence((0, oo), [1, 0, -1, 0], periodical=True))
1 - x**2/2 + x**4/24 + ...
from source function
>>> s = TaylorSeries(source_function=cos(x))
1 - x**2/2 + x**4/24 + ...
The same as Series
(draft variants, see also issue 2026 )
Suppose ts is some series:
>>> ts = TaylorSeries(sequence = Sequence((0, oo), [1, 0, -1, 0], periodical=True))
>>> ts
1 - x**2/2 + x**4/24 + ...
By substitution I can obtain the Sum object:
>>> ts.subs(x, 1)
1 - 1/2 + 1/24 + ...
or calculated Sum
>>> ts(1)
0.540302305868140
or more with intelligibly
>>> ts.subs(x, 1).simplyfy()
cos(1)
-
Determine what is the kind of series of expression will be
-
Determine if LaurentSeries has principal part or not. If not then it is a Taylor. This can be used internally and must be fast.
-
Isolated tasks are the operations over the fields NAME_Series (NAME_Polynomial, NAME_Expansion).
It is necessary first
-
Sequences class
-
representation of Derivative of function at some (no zero) point (issue 1620).
-
representation of composition of functions while differentiation (issue 1660).
-
The class TaylorExpansion can be used even now (replaced little by little in core), with present algorithm of recursive expansion of complexes functions - for effective multiplication it will be easy fix (issue 1038).
- Is internal distinguish between PowerSeries (PowerExpansion) and TaylorSeries (TaylorExpantion) needs?
Yes, sometimes (ODE, operators definition) more effective to work with ones, sometimes more convenient with others.
Taylor series are used to define functions and "operators" in diverse areas of mathematics. In particular, this is true in areas where the classical definitions of functions break down. For example, using Taylor series, one may define analytical functions of matrices and operators, such as the matrix exponential or matrix logarithm.
In other areas, such as formal analysis, it is more convenient to work directly with the power series themselves. Thus one may define a solution of a differential equation as a power series which, one hopes to prove, is the Taylor series of the desired solution.
- What does
sin(x).series(kind="taylor") == sin(x).series(kind="power")must yield?
It is also the question about operations with various (but similar) kinds of series, e.g. sin(x).series(kind="taylor") - sin(x).series(kind="power")
Simplification of this subtraction is obviously zero.
-
Series.show(n): show < n terms or show terms that has power < n ?
May be parameter about it must be in that method.
- Convergence analytic