Pretty Printing

Introduction

SymPy is able to display nice-looking formulas on a pure terminal using ascii-art. In addition, When Unicode is available, it uses special better-looking symbols for drawing.

To try it, run isympy in a unicode-capable terminal such as uxterm or gnome-terminal.

$ ./bin/isympy
IPython console for SymPy 0.7.1-git (Python 2.6.6-64-bit) (ground types: python)

These commands were executed:
>>> from __future__ import division
>>> from sympy import *
>>> x, y, z, t = symbols('x y z t')
>>> k, m, n = symbols('k m n', integer=True)
>>> f, g, h = symbols('f g h', cls=Function)
...

Examples

>>> from sympy import *
>>> f = Function('f')
>>> f(x/(y+1), y)  #doctest: +USE_UNICODE
     ⎛  x     ⎞
    f⎜─────, y⎟
     ⎝y + 1   ⎠
>>> sqrt((sqrt(x+1))+1)
       _______________
      /   _______     
    \/  \/ x + 1  + 1 



>>> from sympy import *
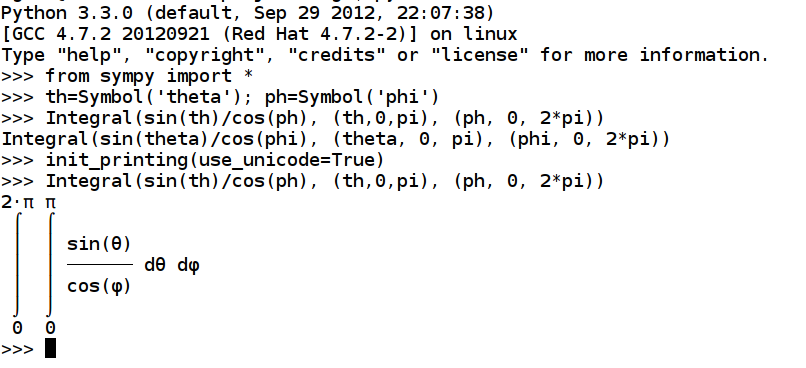
>>> th=Symbol('theta'); ph=Symbol('phi')
>>> Integral(sin(th)/cos(ph), (th,0,pi), (ph, 0, 2*pi)) #doctest: +USE_UNICODE
2⋅π π
 ⌠  ⌠
 ⎮  ⎮ sin(θ)
 ⎮  ⎮ ────── dθ dφ
 ⎮  ⎮ cos(φ)
 ⌡  ⌡
 0  0
>>> Integral(x**2*sin(y), (x,0,1), (y,0,pi))            #doctest: +USE_UNICODE
π 1
⌠ ⌠
⎮ ⎮  2
⎮ ⎮ x ⋅sin(y) dx dy
⌡ ⌡
0 0



>>> from sympy import Symbol
>>> Mul(*[Symbol('theta%i' %i) for i in range(1,5)])    #doctest: +USE_UNICODE
θ₁⋅θ₂⋅θ₃⋅θ₄
>>> Symbol('Y_00')(th,ph)**2 == 1/(4*pi)
False



>>> Matrix([
...   [1/(4*pi), 1],
...   [1, f(x)]
... ])                          #doctest: +USE_UNICODE
⎡ 1       ⎤
⎢───   1  ⎥
⎢4⋅π       ⎥
⎢         ⎥
⎣ 1   f(x)⎦

In different terminal emulators

gnome-terminal:

TBD

KDE Konsole