-
Notifications
You must be signed in to change notification settings - Fork 0
SymPy vs. Maxima
 vs.
vs. 
SymPy and Maxima are Computer algebra systems.
- Computer Algebra System
- A software program that facilitates symbolic mathematics. The core functionality of a CAS is manipulation of mathematical expressions in symbolic form.
Sympy is a Python library for symbolic computation that aims to become a full-featured computer algebra system and to keep the code simple to promote extensibility and comprehensibility.
SymPy was started by Ondřej Čertík in 2005 and he wrote some code in 2006 as well. In 11 March 2007, SymPy was realeased to the public. The latest stable release of SymPy is 0.7.1 (29 July 2011). As of beginning of December 2011 there have been over 150 people who contributed at least one commit to SymPy.
SymPy can be used:
- Inside Python, as a library
- As an interactive command line, using IPython
SymPy is entirely written in Python and does not require any external libraries, but various programs that can extend its capabilites can be installed:
- gmpy, Cython --> speed improvement
- Pyglet, Matplotlib --> 2d and 3d plotting
- IPython --> interactive sessions
SymPy is available online at SymPy Live. The site was developed specifically for SymPy. It is a simple web shell that looks similar to iSymPy under the standard Python interpreter. SymPy Live uses Google App Engine as computational backend.
+ +: small library, pure Python, very functional, extensible, large community.
- -: slow, needs better documentation.
Maxima is a full-featured computer algebra system based on a 1982 version of Macsyma. Macsyma was revolutionary in its day, and many later systems, such as Maple and Mathematica, were inspired by it.
Maxima was created by the MIT Project MAC and Bill Schelter et al. and the development began in 1967. The first public release was in 1998. The latest stable release of Maxima is vesion 5.26.0 (19 December 2011).
Maxima includes a complete programming language with ALGOL-like syntax but Lisp-like semantics. It is written in Common Lisp and can be accessed programmatically and extended, as the underlying Lisp can be called from Maxima. It uses Gnuploy for drawing.
Maxima can be used for:
- differentiation
- integration
- Taylor series
- Laplace transforms
- ordinary differential equations
- systems of linear equations
- polynomials
- sets, lists, vectos, matrices
- tensors
+ +: full scientific stack, generate Fortran code for floating point and arrays, good documentation.
- -: slow, factorization or large numbers or manipulation of extremely large polynomials are slow.
Both SymPy and Maxima are cost free open source CASes. SymPy is released under a modified BSD license, while Maxima is released under the terms of the GNU GPL.
One of the differences between SymPy and Maxima is the fact that Maxima has various GUIs available. wxMaxima is a popular cross-platform GUI using wxWidgets. Starting with version 4.4, the KDE Software Compilation contains Cantor, which can interface with Maxima (along with Sage, R and Kalgebra).
| System | Windows | Mac OS X | Linux | BSD | Solaris | Other |
| SymPy | Yes | Yes | Yes | Yes | Yes | Any system that supports Python |
| Maxima | Yes | Yes | Yes | Yes | Yes | All POSIX platforms with Common Lisp |
Sympy is distributed in various forms. It is possible to download source tarballs and packages from the Google Code page but it is also possible to clone the main Git repository or browse the code online. The only prerequisite is Python since Sympy is Python-based library. It is recommended to install IPython as well, for a better experience.
The Maxima source code can be compiled on many systems, including Windows, Linux and MacOS X. The source code for all systems and precompiled binaries for Windows and Linux are available at the SourceForge file manager.
| System |
Formula editor |
Arbitrary precision |
Calculus | Solvers | ||||
| Integration | Integral transforms* | Equations | Inequalities | Diophantine equations | Differential equations | |||
| SymPy | No | Yes | Yes | No | Yes | Yes | No | Yes |
| Maxima | No | Yes | Yes | Yes | Yes | Yes | No | Yes |
| System | Solvers |
Graph theory |
Number theory |
Quantifier elimination |
Boolean algebra |
Tensors |
| Recurrence relations | ||||||
| SymPy | Yes | No | Yes | No | Yes | Yes |
| Maxima | No | Yes | Yes | Yes | No | Yes |
* Will be available in SymPy 0.7.2
In SymPy, to raise something to a power, you must use **, not ^ as the latter uses the Python meaning, which is xor.
In [1]: (x+1)^2
---------------------------------------------------------------------------
TypeError Traceback (most recent call last)
/home/aoi_hana/sympy/<ipython-input-6-52730bce1577> in <module>()
----> 1 (x+1)^2
TypeError: unsupported operand type(s) for ^: 'Add' and 'int'
In [2]: (x+1)**2
Out[2]:
2
(x + 1)
However, in Maxima, both ^ and ** mean exponentiation:
(%i3) (x+1)**2;
2
(%o3) (x + 1)
(%i4) (x+1)^2;
2
(%o4) (x + 1)
You have to defined symbols in SymPy before you can use them, while in Maxima this is not necessary.
SymPy
>>> x**2 + 2*x + 1
Traceback (most recent call last):
File "<stdin>", line 1, in <module>
NameError: name 'x' is not defined
>>> from sympy import Symbol
>>> x = Symbol('x')
>>> x**2 + 2*x + 1
x**2 + 2*x + 1
Maxima
(%i5) x**2+2*x+1;
2
(%o5) x + 2 x + 1
SymPy
apart(expr, x) must be used to perform partial fraction decomposition. To combine expressions, together(expr, x) is what you need. Here are some examples of these two and other common functions in iSymPy:
In [8]: 1/( (x**2+2*x+1)*(x**2-1) )
Out[8]:
1
───────────────────────
⎛ 2 ⎞ ⎛ 2 ⎞
⎝x - 1⎠⋅⎝x + 2⋅x + 1⎠
In [9]: apart(1/( (x**2+2*x+1)*(x**2-1) ), x)
Out[9]:
1 1 1 1
- ───────── - ────────── - ────────── + ─────────
8⋅(x + 1) 2 3 8⋅(x - 1)
4⋅(x + 1) 2⋅(x + 1)
In [4]: 1/(x**2 + 4*x + 4)*(x**2 - 10*x + 28)
Out[4]:
2
x - 10⋅x + 28
──────────────
2
x + 4⋅x + 4
In [5]: apart(1/(x**2 + 4*x + 4)*(x**2 - 10*x + 28))
Out[5]:
14 52
1 - ───── + ────────
x + 2 2
(x + 2)
In [10]: together(1/(x**2+2*x) - 3/(x+y) + 1/(x+y+z))
Out[10]:
x⋅(x + 2)⋅(x + y) - 3⋅x⋅(x + 2)⋅(x + y + z) + (x + y)⋅(x + y + z)
─────────────────────────────────────────────────────────────────
x⋅(x + 2)⋅(x + y)⋅(x + y + z)
The evalf() method and the N() function can be used to evaluate expressions:
In [20]: pi.evalf() Out[20]: 3.14159265358979 In [23]: N(sqrt(2)*pi, 50) Out[23]: 4.4428829381583662470158809900606936986146216893757
Integrals can be used like regular expressions and support arbitrary precision:
In [24]: Integral(x**(-2*x), (x, 0, oo)).evalf(20) Out[24]: 2.0784499818221828310
The following is an expand example in iSymPy:
In [1]: from sympy import *
In [2]: a, b = symbols('a b')
In [3]: ((a-b)**3).expand()
Out[3]:
3 2 2 3
a - 3⋅a ⋅b + 3⋅a⋅b - b
separate retwrites or separates a power of product to a product of powers but without any expanding, i.e., rewriting products to summations. Notice that the summations are left untouched. If this is not the requested behavior, apply 'expand' to input expressions.
In [14]: separate((a+b)*(c+d))
Out[14]: (a + b)⋅(c + d)
In [15]: separate((a+b)*(c+d)).expand()
Out[15]: a⋅c + a⋅d + b⋅c + b⋅d
In [12]: separate(1/((a+b)*(c+d)))
Out[12]:
1
───────────────
(a + b)⋅(c + d)
In [13]: separate(1/((a+b)*(c+d))).expand()
Out[13]:
1
─────────────────────
a⋅c + a⋅d + b⋅c + b⋅d
Maxima
partfrac(expr, var) expands the expression expr in partial fractions with respect to the main variable var.
(%i3) partfrac(1/((x^2+2*x+1)*(x^2-1)), x);
1 1 1 1
(%o3) - --------- - ---------- - ---------- + ---------
8 (x + 1) 2 3 8 (x - 1)
4 (x + 1) 2 (x + 1)
(%i4) partfrac(1/(x^2+4*x+4)*(x^2-10*x+28), x);
14 52
(%o4) - ----- + -------- + 1
x + 2 2
(x + 2)
expand(expr) expands the expression expr.
(%i8) expand((a-b)^3);
3 2 2 3
(%o8) - b + 3 a b - 3 a b + a
distrib(expr) distributes sums over products. It differs from expand in that it works at only the top level of an expression, i.e., it doesn't recurse and it is faster than expand. It differs from multthru in that it expands all sums at that level.
(%i9) distrib((a+b)*(c+d));
(%o9) b d + a d + b c + a c
(%i10) multthru((a+b)*(c+d));
(%o10) (b + a) d + (b + a) c
(%i11) distrib(1/((a+b)*(c+d)));
1
(%o11) ---------------
(b + a) (d + c)
(%i12) expand(1/((a+b)*(c+d)), 1, 0);
1
(%o12) ---------------------
b d + a d + b c + a c
SymPy
Limits in SymPy have the following syntax: limit(function, variable, point). Here are some examples:
Limit of f(x)= sin(x)/x as x -> 0
In [20]: from sympy import *
In [21]: x = Symbol('x')
In [22]: limit(sin(x)/x, x, 0)
Out[22]: 1
Limit of f(x)= 2*x+1 as x -> 5/2
In [24]: limit(2*x+1, x, S(5)/2) # The *S()* method must be used for 5/2 to be Rational in SymPy Out[24]: 6
You can also compute the left and right limits of an expression with the dir="+/-" argument.
In [5]: limit(1/x, x, oo) Out[5]: 0 In [6]: limit(1/x, x, 0, dir="+") Out[6]: ∞ In [7]: limit(1/x, x, 0, dir="-") Out[7]: -∞
Maxima
limit(expr, x, val, dir) computes the limit of expr as the real variable x approaches the value val from the direction dir.
(%i4) limit(sin(x)/x, x, 0); (%o4) 1 (%i5) limit(2*x+1,x, 5/2); (%o5) 6 (%i13) limit(1/x, x, inf); (%o13) 0 (%i14) limit(1/x, x, 0, plus); (%o14) inf (%i15) limit(1/x, x, 0, minus); (%o15) minf
tlimit(expr, x, val, dir) takes the limit of the Taylor series expansion of expr in x at var from direction dir.
(%i13) tlimit (1/cos(x^2), x, 0); (%o13) 1
SymPy
In [1]: from sympy import *
In [2]: x = Symbol('x')
In [3]: diff(cos(x**3), x)
Out[3]:
2 ⎛ 3⎞
-3⋅x ⋅sin⎝x ⎠
In [4]: diff(atan(2*x), x)
Out[4]:
2
────────
2
4⋅x + 1
In [6]: diff(1/tan(x), x)
Out[6]:
2
- tan (x) - 1
─────────────
2
tan (x)
This is how you create a Bessel function of the first kind object and differentiate it:
In [7]: from sympy import besselj, jn
In [8]: from sympy.abc import z, n
In [9]: b = besselj(n, z)
In [10]: # Differentiate it:
In [11]: b.diff(z)
Out[11]:
besselj(n - 1, z) besselj(n + 1, z)
───────────────── - ─────────────────
2 2
Maxima
diff(expr, x_1, n_1, ..., x_m, n_m) returns the derivative or differential of expr with respect to some or all variables in expr.
(%i2) diff(cos(x^3), x);
2 3
(%o2) - 3 x sin(x )
(%i3) diff(atan(2*x), x);
2
(%o3) --------
2
4 x + 1
(%i4) diff(1/tan(x), x);
2
sec (x)
(%o4) - -------
2
tan (x)
del(x) represents the differential of the variable x. diff returns an expression containing del if an independent variable is not specified.
(%i5) diff(log(x));
del(x)
(%o5) ------
x
(%i7) diff(exp(x*y));
x y x y
(%o7) x %e del(y) + y %e del(x)
(%i8) diff(x*y*z);
(%o8) x y del(z) + x z del(y) + y z del(x)
bessel_j(v,z) returns the bessel function of the first kind of order v and argument z.
(%i1) diff(bessel_j(v, z), z);
bessel_j(v - 1, z) - bessel_j(v + 1, z)
(%o1) ---------------------------------------
2
SymPy
The syntax for series expansion is: .series(var, point, order):
In [27]: from sympy import *
In [28]: x = Symbol('x')
In [29]: cos(x).series(x, 0, 14)
Out[29]:
2 4 6 8 10 12
x x x x x x ⎛ 14⎞
1 - ── + ── - ─── + ───── - ─────── + ───────── + O⎝x ⎠
2 24 720 40320 3628800 479001600
In [30]: (1/cos(x**2)).series(x, 0, 14)
Out[30]:
4 8 12
x 5⋅x 61⋅x ⎛ 14⎞
1 + ── + ──── + ────── + O⎝x ⎠
2 24 720
It is possible to make use of series(x*cos(x), x) by creating a wrapper around Basic.series().
In [31]: from sympy import Symbol, cos, series
In [32]: x = Symbol('x')
In [33]: series(cos(x), x)
Out[33]:
2 4
x x ⎛ 6⎞
1 - ── + ── + O⎝x ⎠
2 24
This module also implements automatic keeping track of the order of your expansion.
In [1]: from sympy import Symbol, Order
In [2]: x = Symbol('x')
In [3]: Order(x) + x**2
Out[3]: O(x)
In [4]: Order(x) + 28
Out[4]: 28 + O(x)
Maxima
The taylor(expr, x, a, n) function expands the expression expr in a truncated Taylor or Laurent series in the variable x around the point a, containing terms through (x - a)^n.
(%i4) taylor (cos(x), x, 0, 14);
2 4 6 8 10 12 14
x x x x x x x
(%o4)/T/ 1 - -- + -- - --- + ----- - ------- + --------- - ----------- + . . .
2 24 720 40320 3628800 479001600 87178291200
(%i5) taylor (1/cos(x^2), x, 0, 14);
4 8 12
x 5 x 61 x
(%o5)/T/ 1 + -- + ---- + ------ + . . .
2 24 720
SymPy
The integrals module in SymPy implements methods calculating definite and indefinite integrals of expressions. Principal method in this module is integrate():
- integrate(f, x) returns the indefinite integral
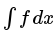
- integrate(f, (x, a, b)) returns the definite integral
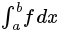
SymPy can integrate:
- polynomial functions:
In [6]: from sympy import *
In [7]: import sys
In [8]: from sympy import init_printing
In [9]: init_printing(use_unicode=False, wrap_line=False, no_global=True)
In [10]: x = Symbol('x')
In [11]: integrate(x**2 + 2*x + 4, x)
3
x 2
── + x + 4⋅x
3
- rational functions:
In [1]: integrate((x+1)/(x**2+4*x+4), x)
Out[1]:
1
log(x + 2) + ─────
x + 2
- exponential-polynomial functions:
In [5]: integrate(5*x**2 * exp(x) * sin(x), x)
Out[5]:
2 x 2 x x x
5⋅x ⋅ℯ ⋅sin(x) 5⋅x ⋅ℯ ⋅cos(x) x 5⋅ℯ ⋅sin(x) 5⋅ℯ ⋅cos(x)
────────────── - ────────────── + 5⋅x⋅ℯ ⋅cos(x) - ─────────── - ──────────
2 2 2 2
- non-elementary integrals:
In [11]: integrate(exp(-x**2)*erf(x), x)
___ 2
╲╱ π ⋅erf (x)
─────────────
4
Other examples:
In [8]: integrate(sin(x)**3, x)
Out[8]:
3
cos (x)
─────── - cos(x)
3
In [9]: integrate(cos(x)**2*exp(x), (x, 0, pi))
Out[9]:
π
3 3⋅ℯ
- ─ + ────
5 5
Here is an example of a definite integral (Calculate 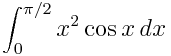 ):
):
In [1]: integrate(x**2 * cos(x), (x, 0, pi/2))
Out[1]:
2
π
-2 + ──
4
In [6]: integrate(cot(x)**4, (x, pi/2, pi/4))
Out[6]:
π 2
- ─ + ─
4 3
Maxima
integrate(expr,x) and integrate(expr,x,a,b) attempt to symbolically compute the intrgral of expr with respect to x. integrate(expr, x) is an indefinite integral, while integrate(expr, x, a, b) is a definite integral, with limits of integration a and b.
Maxima can integrate:
- polynomial functions:
(%i5) integrate(x^2+2*x+4,x);
3
x 2
(%o5) -- + x + 4 x
3
- rational functions:
(%i6) integrate((x+1)/(x^2+4*x+4),x);
1
(%o6) log(x + 2) + -----
x + 2
- exponential-polynomial functions:
(%i7) integrate(5*x^2*exp(x)*sin(x),x);
2 x 2 x
5 ((x - 1) %e sin(x) + (- x + 2 x - 1) %e cos(x))
(%o7) -----------------------------------------------------
2
- non-elementary integrals:
(%i8) integrate(exp(-x^2)*erf(x),x);
2
sqrt(%pi) erf (x)
(%o8) -----------------
4
Other examples:
(%i3) integrate(sin(x)^3,x);
3
cos (x)
(%o3) ------- - cos(x)
3
(%i4) integrate(cos(x)^2*exp(x), x, 0, %pi);
%pi
3 %e 3
(%o4) ------- - -
5 5
defint(expr,x,a,b) attempts to compute a definite integral. defint returns a symbolic expression, either the computed integral or the noun form of the integral.
(%i1) defint(x^2*cos(x), x, 0, %pi/2);
2
%pi - 8
(%o1) --------
4
(%i2) defint(cot(x)^4, x, %pi/2, %pi/4);
2 %pi
(%o2) - - ---
3 4
SymPy
In [1]: from sympy import Symbol, exp, I
In [2]: x = Symbol("x")
In [3]: exp(I*2*x).expand()
Out[3]:
2⋅ⅈ⋅x
ℯ
In [4]: exp(I*2*x).expand(complex=True)
Out[4]:
-2⋅im(x) -2⋅im(x)
ⅈ⋅ℯ ⋅sin(2⋅re(x)) + ℯ ⋅cos(2⋅re(x))
In [5]: x = Symbol("x", real=True)
In [6]: exp(I*2*x).expand(complex=True)
Out[6]: ⅈ⋅sin(2⋅x) + cos(2⋅x)
In [7]: exp(-2 + 3*I*x).expand(complex=True)
Out[7]:
-2 -2
ⅈ⋅ℯ ⋅sin(3⋅x) + ℯ ⋅cos(3⋅x)
Complex number division in iSymPy:
In [4]: from sympy import I In [5]: ((2 + 3*I)/(3 + 7*I)).expand(complex=True) Out[5]: 27 5⋅ⅈ ── - ─── 58 58
Maxima
rectform(expr) returns an expression a + b %i equivalent to expr, such that a and b are purely real.
(%i1) rectform(exp(2*i*x));
2 i x
(%o1) %e
(%i1) rectform(exp(%i*2*x));
(%o1) %i sin(2 x) + cos(2 x)
Complex number division in Maxima:
(%i8) rectform((2+3*%i)/(3+7*%i));
27 5 %i
(%o8) -- - ----
58 58
SymPy
trigonometric
In [1]: cos(x-y).expand(trig=True)
Out[1]: sin(x)⋅sin(y) + cos(x)⋅cos(y)
In [2]: cos(2*x).expand(trig=True)
Out[2]:
2
2⋅cos (x) - 1
In [3]: sinh(I*x**2)
Out[3]:
⎛ 2⎞
ⅈ⋅sin⎝x ⎠
In [11]: sinh(acosh(x))
Out[11]:
_______ _______
╲╱ x - 1 ⋅╲╱ x + 1
zeta function
In [4]: zeta(5, x**2) Out[4]: ⎛ 2⎞ ζ⎝5, x ⎠ In [5]: zeta(5, 2) Out[5]: ζ(5, 2) In [6]: zeta(4, 1) Out[6]: 4 π ── 90 In [5]: zeta(28).evalf() Out[5]: 1.00000000372533
factorials and gamma function
In [7]: a = Symbol('a')
In [8]: b = Symbol('b', integer=True)
In [9]: factorial(a)
Out[9]: a!
In[10]: factorial(10)
Out[10]: 3628800
In [11]: N(gamma(S(25)/10), 31)
Out[11]: 1.329340388179137020473625612506
polynomials
In [14]: chebyshevt(8,x)
Out[14]:
8 6 4 2
128⋅x - 256⋅x + 160⋅x - 32⋅x + 1
In [15]: legendre(3, x)
Out[15]:
3
5⋅x 3⋅x
──── - ───
2 2
In [16]: hermite(3, x)
Out[16]:
3
8⋅x - 12⋅x
Maxima
trigonometric
trigexpand(expr) expands trigonometric and hyperbolic functions of sums of angles and of multiple angles occurring in expr.
(%i1) x+sin(3*x)/sin(x), trigexpand=true,expand;
2 2
(%o1) - sin (x) + 3 cos (x) + x
(%i2) trigexpand(sin(10*x+y));
(%o2) cos(10 x) sin(y) + sin(10 x) cos(y)
(%i3) cos(x-y),trigexpand=true,trigexpandplus=true,expand;
(%o3) sin(x) sin(y) + cos(x) cos(y)
(%i2) cos(2*x),trigexpand=true,trigexpandtimes=true,expand;
2 2
(%o2) cos (x) - sin (x)
(%i1) declare (x, imaginary)$
(%i2) [ featurep (x, imaginary), featurep (x, real)];
(%o2) [true, false]
(%i3) sinh(%i * x^2);
2
(%o3) %i sin(x )
(%i4) sinh(acosh(x));
(%o4) sqrt(x - 1) sqrt(x + 1)
When halfangles is true, trigonometric functions of arguments expr/2 are simplified to functions of expr.
(%i1) halfangles:false;
(%o1) false
(%i2) sin(x/2);
x
(%o2) sin(-)
2
(%i3) halfangles:true;
(%o3) true
(%i4) sin(x/2);
x
floor(-----)
2 %pi
(- 1) sqrt(1 - cos(x))
(%o4) ----------------------------------
sqrt(2)
(%i7) assume(x>0, x<2*%pi)$
(%i8) sin(x/2);
sqrt(1 - cos(x))
(%o8) ----------------
sqrt(2)
zeta function
zeta(n) returns the Riemann zeta function. The Riemann zeta function distributes over lists, matrices and equations.
(%i5) zeta(4);
4
%pi
(%o5) ----
90
(%i6) zeta(28);
28
6785560294 %pi
(%o6) ------------------------
564653660170076273671875
factorials and gamma function
(%i13) factorial(a);
(%o13) a!
(%i14) factorial(10);
(%o14) 3628800
(%i15) gamma(25/10);
3 sqrt(%pi)
(%o15) -----------
4
polynomials
chebyshev_t(n,x) returns the Chebyshev function of the first kind.
(%i21) chebyshev_t(8,x);
8 7 6 5 4 3 2
(%o21) - 64 (1 - x) + 128 (1 - x) - 1024 (1 - x) + 3328 (1 - x) - 5632 (1 - x) + 5280 (1 - x) - 2688 (1 - x) + 672 (1 - x) + 1
legendre_p(n,x) returns the Legendre polynomial of the first kind.
(%i19) legendre_p(3,x);
3 2
5 (1 - x) 15 (1 - x)
(%o19) - 6 (1 - x) - ---------- + ----------- + 1
2 2
hermite(n,x) returns the Hermite polynomial.
(%i17) hermite(3,x);
2
2 x
(%o17) - 12 x (1 - ----)
3
SymPy
In iSymPy:
In [10]: f(x).diff(x, x) + f(x)
Out[10]:
2
d
f(x) + ───(f(x))
2
dx
dsolve(eq, f(x), hint) solves ordinary differential euqtion eq for function f(x), using method hint.
In [1]: from sympy import Function, dsolve, Eq, Derivative, sin, cos
In [2]: from sympy.abc import x
In [3]: f = Function('f')
In [5]: dsolve(Derivative(f(x),x,x)+9*f(x), f(x))
Out[5]: f(x) = C₁⋅sin(3⋅x) + C₂⋅cos(3⋅x)
In [7]: dsolve(sin(x)*cos(f(x)) + cos(x)*sin(f(x))*f(x).diff(x), f(x),
...: hint='best')
Out[7]:
⎛ C₁ ⎞
f(x) = acos⎜──────⎟
⎝cos(x)⎠
In [11]: dsolve(f(x).diff(x, x) + f(x), f(x))
Out[11]: f(x) = C₁⋅sin(x) + C₂⋅cos(x)
Maxima
Maxima's ordinary differential equation (ODE) solver ode2 solves elementary linear OEs of first and second order. The function contrib)ode extends ode2 with additional methods for linear and non-linear first order ODEs and linear homogeneous second order ODEs. This package must be loaded with the command load('contrib_ode) before use.
(%i2) load('contrib_ode)$
(%i3) eqn:x*'diff(y,x)^2-(1+x*y)*'diff(y,x)+y=0;
dy 2 dy
(%o3) x (--) - (x y + 1) -- + y = 0
dx dx
(%i4) contrib_ode(eqn,y,x);
dy 2 dy
(%t4) x (--) - (x y + 1) -- + y = 0
dx dx
first order equation not linear in y'
x
(%o4) [y = log(x) + %c, y = %c %e ]
(%i5) method;
(%o5) factor
The function desolve(eqn, x) solves systems of linear ordinary differential equations using Laplace transform.
(%i1) 'diff(f(x),x)='diff(g(x),x)+sin(x);
d d
(%o1) -- (f(x)) = -- (g(x)) + sin(x)
dx dx
(%i2) 'diff(g(x),x,2)='diff(f(x),x)-cos(x);
2
d d
(%o2) --- (g(x)) = -- (f(x)) - cos(x)
2 dx
dx
(%i5) atvalue('diff(g(x),x),x=0,a);
(%o5) a
(%i6) atvalue(f(x),x=0,1);
(%o6) 1
(%i7) desolve([%o1,%o2],[f(x),g(x)]);
x x
(%o7) [f(x) = a %e - a + 1, g(x) = cos(x) + a %e - a + g(0) - 1]
SymPy
In iSymPy:
In [3]: solve(x**3 + 2*x**2 - 1, x) Out[3]: ⎡ ___ ___ ⎤ ⎢ 1 ╲╱ 5 ╲╱ 5 1⎥ ⎢-1, - ─ + ─────, - ───── - ─⎥ ⎣ 2 2 2 2⎦ In [5]: solve( [x**2 + 4*y**2 -2, -10*x + 2*y -15], [x, y]) Out[5]: ⎡⎛ ____ ____ ⎞ ⎛ ____ ____ ⎞⎤ ⎢⎜ 150 ╲╱ 23 ⋅ⅈ 15 5⋅╲╱ 23 ⋅ⅈ ⎟ ⎜ 150 ╲╱ 23 ⋅ⅈ 15 5⋅╲╱ 23 ⋅ ⎟⎥ ⎢⎜- ─── - ────────, ─── - ──────────⎟, ⎜- ─── + ────────, ─── + ────────── ⎟⎥ ⎣⎝ 101 101 202 101 ⎠ ⎝ 101 101 202 101 ⎠⎦
Maxima
solve([enq_1, ..., eqn_n],[x_1, ...,x_n]) solve the algebraic equation expr for the variable x and returns a list of solution equations in x.
(%i1) solve(x^3+2*x^2-1,x);
sqrt(5) + 1 sqrt(5) - 1
(%o1) [x = - -----------, x = -----------, x = - 1]
2 2
(%i3) solve([x^2+4*y^2-2, -10*x+2*y-15], [x, y]);
sqrt(23) %i + 150 10 sqrt(23) %i - 15
(%o3) [ [x = - -----------------, y = - -------------------],
101 202
sqrt(23) %i - 150 10 sqrt(23) %i + 15
[x = -----------------, y = -------------------] ]
101 202
SymPy
In SymPy, matrices are created as instances from the Matrix class:
In [1]: from sympy import Matrix In [2]: Matrix([ [1, 0 , 0], [0, 1, 0], [0, 0, 1] ]) Out[2]: ⎡1 0 0⎤ ⎢ ⎥ ⎢0 1 0⎥ ⎢ ⎥ ⎣0 0 1⎦
It is possible to slice submatrices, since this is Python:
In [4]: M = Matrix(2, 3, [1, 2, 3, 4, 5, 6]) In [5]: M[0:2,0:2] Out[5]: ⎡1 2⎤ ⎢ ⎥ ⎣4 5⎦ In [6]: M[1:2,2] Out[6]: [6] In [7]: M[:,2] Out[7]: ⎡3⎤ ⎢ ⎥ ⎣6⎦
One basic operation involving matrices is the determinant:
In [8]: M = Matrix(( [2, 5, 6], [4, 7, 10], [1, 0, 3] )) In [9]: M.det() Out[9]: -10
print_nonzero(symb='x') shows location of non-zero entries for fast shape lookup.
In [10]: M = Matrix(( [2, 0, 0, 1, 0], [3, 5, 0, 1, 0], [10, 4, 0, 1, 2], [1, 6, 0, 0, 0], [0, 4, 0, 2, 2] )) In [12]: M Out[12]: ⎡2 0 0 1 0⎤ ⎢ ⎥ ⎢3 5 0 1 0⎥ ⎢ ⎥ ⎢10 4 0 1 2⎥ ⎢ ⎥ ⎢1 6 0 0 0⎥ ⎢ ⎥ ⎣0 4 0 2 2⎦ In [13]: M.print_nonzero() [X X ] [XX X ] [XX XX] [XX ] [ X XX]
Matrix transposition with transpose():
In [14]: from sympy import Matrix, I In [15]: m = Matrix(( (1,2+I), (3,4) )) In [16]: m Out[16]: ⎡1 2 + ⅈ⎤ ⎢ ⎥ ⎣3 4 ⎦ In [17]: m.transpose() Out[17]: ⎡ 1 3⎤ ⎢ ⎥ ⎣2 + ⅈ 4⎦ In [19]: m.T == m.transpose() Out[19]: True
The multiply_elementwise(b) method returns the Hadamard product (elementwise product) of A and B:
In [14]: import sympy In [15]: A = sympy.Matrix([ [1, 3, 20], [1, 18, 3] ]) In [17]: B = sympy.Matrix([ [0, 5, 10], [4, 20, 6] ]) In [18]: print A.multiply_elementwise(B) [0, 15, 200] [4, 360, 18]
Maxima
This is how you create a matrix in Maxima:
(%i5) a: matrix ([1, 0, 0], [0, 1, 0], [0, 0, 1]);
[ 1 0 0 ]
[ ]
(%o5) [ 0 1 0 ]
[ ]
[ 0 0 1 ]
Maxima can return the identity matrix with diagmatrix(n, x) and ident(n) as well:
(%i9) diagmatrix(3, 1);
[ 1 0 0 ]
[ ]
(%o9) [ 0 1 0 ]
[ ]
[ 0 0 1 ]
(%i10) ident(3);
[ 1 0 0 ]
[ ]
(%o10) [ 0 1 0 ]
[ ]
[ 0 0 1 ]
coefmatrix([eqn_1, ..., eqn_m],[x_1, ..., x_n]) returns the coefficient matrix for the variables x_1, ..., x_n of the system of linear equations eqn_1, ..., eqn_m.
(%i1) m: [2*x - (a-1)*y = 5*b, b*y + a*x = 3]$
(%i2) coefmatrix(m, [x, y]);
[ 2 1 - a ]
(%o2) [ ]
[ a b ]
col(M, i) returns the i'th column of the matrix M. The row(M,i) function returns the i'th row of the matrix M. The return values are matrices.
(%i6) col(a,2);
[ 0 ]
[ ]
(%o6) [ 1 ]
[ ]
[ 0 ]
(%i30) row(ident(3),2);
(%o30) [ 0 1 0 ]
transpose(M) returns the transpose of M.
(%i31) m: matrix([1, 2+%i], [3, 4])$
(%i32) transpose(m);
[ 1 3 ]
(%o32) [ ]
[ %i + 2 4 ]
determinant(M) computes the determinant of M by a method similar to Gaussian elimination.
(%i7) m: matrix ([2, 5, 6], [4, 7, 10], [1, 0, 3])$ (%i8) determinant(m); (%o8) - 10
When domxexpt is true, a matrix exponential, exp(M) where M is a matrix, is interpreted as a matrix with element. Otherwise exp(M) evaluates to exp(ev(M)).
(%i16) m: matrix ([5, %pi],[2+%i, sqrt(4)]);
[ 5 %pi ]
(%o16) [ ]
[ %i + 2 2 ]
(%i17) domxexpt: false$
(%i18) (3-c)^m;
[ 5 %pi ]
[ ]
[ %i + 2 2 ]
(%o18) (3 - c)
(%i19) domxexpt: true$
(%i20) (3-c)^m;
[ 5 %pi ]
[ (3 - c) (3 - c) ]
(%o20) [ ]
[ %i + 2 2 ]
[ (3 - c) (3 - c) ]
The example below displays a matrix base to a matrix exponent. This is not carried out element by element.
(%i26) x: matrix([17, 3], [-8, 11])$
(%i27) y: matrix([%pi, %e], [b, c])$
(%i28) x^y;
[ %pi %e ]
[ ]
[ b c ]
[ 17 3 ]
(%o28) [ ]
[ - 8 11 ]
SymPy
The geometry module can be used to create two-dimensional geometrical entities and query information about them. These entities are available:
- Point
- Line, Ray, Segment
- Ellipse, Circle
- Polygon, RegularPolygon, Triangle
Check if points are collinear:
In [37]: from sympy import * In [38]: from sympy.geometry import * In [39]: x = Point(0, 0) In [40]: y = Point(3, 1) In [41]: z = Point(5, 5) In [42]: Point.is_collinear(x, y, z) Out[42]: False In [43]: Point.is_collinear(x, z) Out[43]: True
Segment declaration, slope, length, midpoint:
In [1]: import sympy In [2]: from sympy import Point In [3]: from sympy.abc import s In [4]: from sympy.geometry import Segment In [5]: Segment( (1, 2), (2, -3)) Out[5]: ((1,), (2,)) In [6]: s = Segment(Point(4, 3), Point(1, 1)) In [7]: s Out[7]: ((1,), (4,)) In [8]: s.points Out[8]: ((1,), (4,)) In [9]: s.slope Out[9]: 2/3 In [10]: s.length Out[10]: ____ ╲╱ 13 In [11]: s.midpoint Out[11]: (5/2,)
Maxima
points([[x1,y1], [x2,y2],...]) raws points in 2D and 3D.
(%i1) load(draw)$
(%o1) draw2d(
key = "Small points",
points(makelist([random(20),random(50)],k,1,10)),
point_type = circle,
point_size = 3,
points_joined = true,
key = "Great points",
points(makelist(k,k,1,20),makelist(random(30),k,1,20)),
point_type = filled_down_triangle,
key = "Automatic abscissas",
color = red,
points([2,12,8]))$
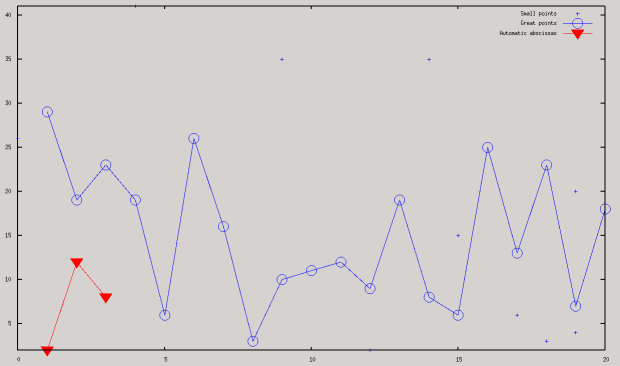
(%i5) load(draw)$ (%i6) draw3d(spherical(1,a,0,2*%pi,z,0,%pi))$
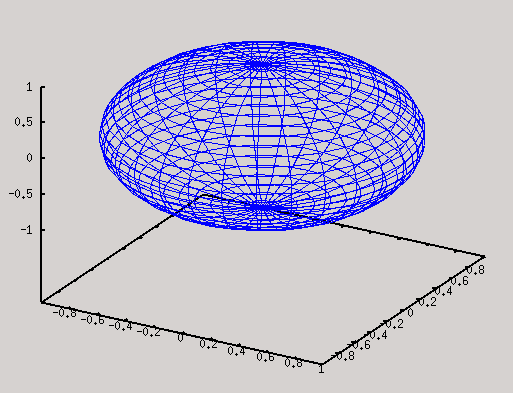
SymPy
Using the .match method and the Wild class you can perform pattern matching on expressions. The method returns a dictionary with the needed substitutions. Here is an example:
In [11]: from sympy import *
In [12]: x = Symbol('x')
In [13]: y = Wild('y')
In [14]: (10*x**3).match(y*x**3)
Out[14]: {y: 10}
In [15]: s = Wild('s')
In [16]: (x**4).match(y*x**s)
Out[16]: {s: 4, y: 1}
SymPy returns None if the match is unsuccessful:
In [19]: print (x+1).match(y**x) None
Maxima
defmatch(progname, pattern, x_1, ..., x_n) defines a function progname(expr, x_1, ..., x_n) which tests expr to see if it matches pattern.
(%i1) matchdeclare(a, lambda ([e], e#0 and freeof(x,e)), b, freeof(x));
(%o1) done
(%i2) defmatch(linearp, a*x+b, x);
(%o2) linearp
(%i3) linearp(3*z+(y+1)*z+y^2,z);
2
(%o3) [b = y , a = y + 4, x = z]
(%i4) a;
(%o4) y + 4
(%i5) b;
2
(%o5) y
(%i6) x;
(%o6) x
Define a function checklimits(expr) which tests expr to see if it is a definite integral.
(%i1) matchdeclare([a,f], true);
(%o1) done
(%i2) constinterval(l, h) := constantp (h-l);
(%o2) constinterval(l, h) := constantp(h - l)
(%i3) matchdeclare(b, constinterval(a));
(%o3) done
(%i4) matchdeclare(x, atom);
(%o4) done
(%i5) simp : false;
(%o5) false
(%i6) defmatch(checklimits, 'integrate(f, x, a, b));
(%o6) checklimits
(%i7) simp : true;
(%o7) true
(%i8) 'integrate(sin(t), t, %pi+x, 2*%pi+x);
x + 2 %pi
/
[
(%o8) I sin(t) dt
]
/
x + %pi
(%i9) checklimits(%);
(%o9) [b = x + 2 %pi, a = x + %pi, x = t, f = sin(t)]
(%i10) 'integrate(cos(t), t);
/
[
(%o10) I cos(t) dt
]
/
(%i11) checklimits(%);
(%o11) false
SymPy
There are many ways of printing mathematical expressions. Three of the most common methods are:
- Standard printing
- Pretty printing using the pprint() function
- Pretty printing using the init_printing() method
Standard printing is the return value of str(expression):
>>> from sympy import Integral # Python session >>> from sympy.abc import c >>> print c**3 c**3 >>> print 2/c 2/c >>> print Integral(c**2+2*c, c) Integral(c**2 + 2*c, c)
Pretty printing is a nice ascii-art printing with the help of a pprint function.
In [1]: from sympy import Integral, pprint # IPython session (pprint enabled by default) In [2]: from sympy.abc import c In [3]: pprint(c**3) 3 c In [4]: pprint(2/c) 2 ─ c In [5]: pprint(Integral(c**2+2*c, c)) ⌠ ⎮ ⎛ 2 ⎞ ⎮ ⎝c + 2⋅c⎠ dc ⌡
However, the proper way to set up pretty printing in SymPy is to use init_printing(pretty_print=True, order=None, use_unicode=None, wrap_line=None, num_columns=None, no_global=False, ip=None):
>>> from sympy import init_printing
>>> init_printing(use_unicode=False, wrap_line=False, no_global=True)
>>> from sympy import Integral, Symbol
>>> x = Symbol('x')
>>> Integral(x**3+2*x+1, x)
/
|
| / 3 \
| \x + 2*x + 1/ dx
|
/
>>> init_printing(pretty_print=True)
>>> Integral(x**3+2*x+1, x)
⌠
⎮ ⎛ 3 ⎞
⎮ ⎝x + 2⋅x + 1⎠ dx
⌡
Maxima
There are various methods to print expressions in Maxima:
print(exp_1, ..., expr_n) evaluates and displays expr_1, ..., expr_n one after another, from left to rght, starting at the left edge of the console display.
(%i22) print (c^3)$
3
c
(%i23) print(2/c)$
2
-
c
(%i24) print('integrate(c^2+2*c,c))$
/
[ 2
I (c + 2 c) dc
]
/
grind(expr) prints epr to the console in a form suitable for input to Maxima. grind always returns done.
(%i25) matrix ([2, 3, 4], [5, 6, 7]);
[ 2 3 4 ]
(%o25) [ ]
[ 5 6 7 ]
(%i26) grind(%);
matrix([2,3,4],[5,6,7])$
(%o26) done
(%i28) expr: expand((aa+bb)^10);
10 9 2 8 3 7 4 6 5 5
(%o28) bb + 10 aa bb + 45 aa bb + 120 aa bb + 210 aa bb + 252 aa bb
6 4 7 3 8 2 9 10
+ 210 aa bb + 120 aa bb + 45 aa bb + 10 aa bb + aa
(%i29) grind(expr);
bb^10+10*aa*bb^9+45*aa^2*bb^8+120*aa^3*bb^7+210*aa^4*bb^6+252*aa^5*bb^5
+210*aa^6*bb^4+120*aa^7*bb^3+45*aa^8*bb^2+10*aa^9*bb+aa^10$
(%o29) done
tcl_output(list,i0,skip) prints elements of a list enclosed by curly braces { }, suitable as part of a program in the Tcl/Tk language.
(%i14) tcl_output([1, 2, 3, 4, 5, 6], 2, 3)$
{2.000000000 5.000000000
}
tex(expr, destination) prints a representation of an expression suitable for the TeX document preparation systems. destination may be an output stream or file name.
(%i16) 'integrate(x^3+2*x+1,x);
/
[ 3
(%o16) I (x + 2 x + 1) dx
]
/
(%i18) tex(%o16);
$$\int {x^3+2\,x+1}{\;dx}\leqno{\tt (\%o16)}$$
(%o18) (\%o16)
(%i19) integrate(1/(1+x^3), x);
2 x - 1
2 atan(-------)
log(x - x + 1) sqrt(3) log(x + 1)
(%o19) - --------------- + ------------- + ----------
6 sqrt(3) 3
(%i20) tex(%o19);
$$-{{\log \left(x^2-x+1\right)}\over{6}}+{{\arctan \left({{2\,x-1
}\over{\sqrt{3}}}\right)}\over{\sqrt{3}}}+{{\log \left(x+1\right)
}\over{3}}\leqno{\tt (\%o19)}$$
(%o20) (\%o19)
SymPy
Pyglet is required to use the plotting function of SymPy in 2d and 3d. Here is an example:
>>> from sympy import symbols, Plot, cos, sin
>>> x, y = symbols('x y')
>>> Plot(sin(x*10)*cos(y*5) - x*y)
[0]: -x*y + sin(10*x)*cos(5*y), 'mode=cartesian'
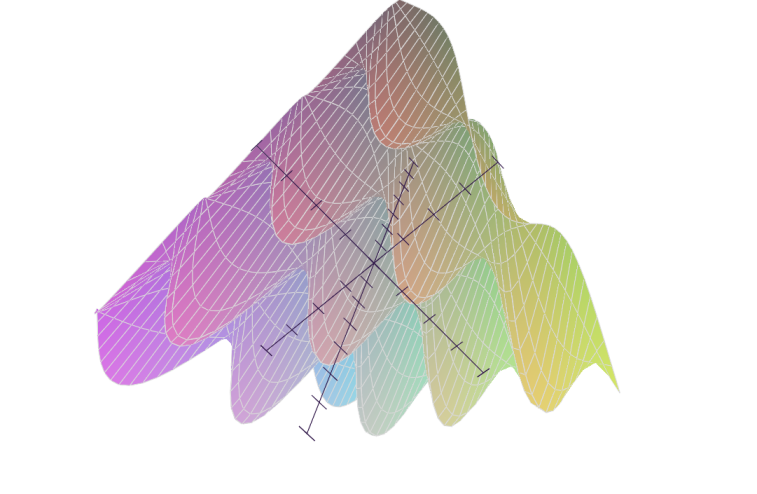
In[1]: Plot(cos(x*y*10)) Out[1]: [0]: cos(10*x*y), 'mode=cartesian'
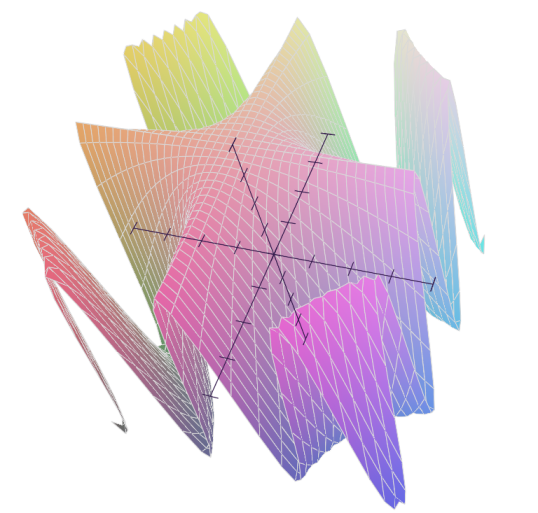
In [22]: Plot(1*x**2, [], [x], 'mode=cylindrical') # [unbound_theta,0,2*Pi,40], [x,-1,1,20] Out[22]: [0]: x**2, 'mode=cylindrical'
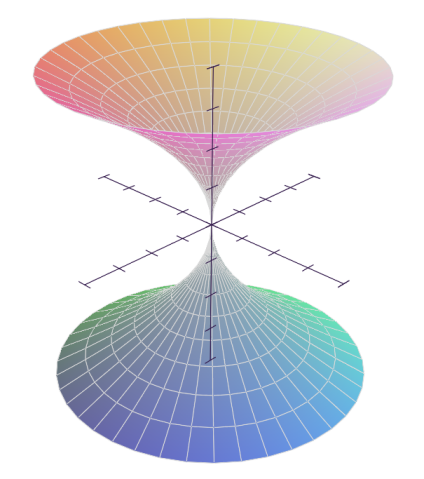
Maxima
Here are some examples of plotting in Maxima:
(%i1) plot3d(sin(x*10)*cos(y*5)-x*y, [x, -1, 1], [y, -1, 1])$
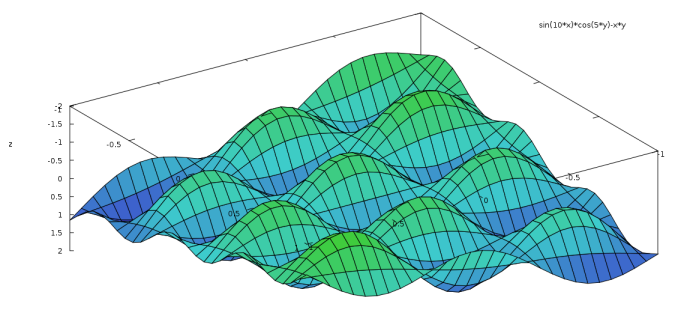
(%i2) plot3d(cos(10*x*y), [x, -1, 1], [y, -1, 1], [palette,[value,0.65,0.7,0.1,0.9] ])$
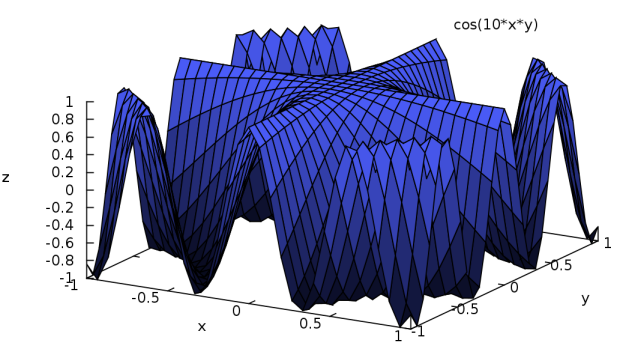
(%i1) plot3d ( 5, [theta, 0, %pi], [phi, 0, 2*%pi],
[plot_format,xmaxima],
[transform_xy, spherical_to_xyz],
[palette,[value,0.65,0.7,0.1,0.9] ])$
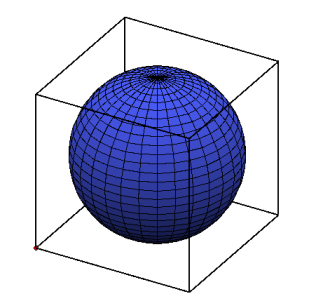
(%i1) plot3d (log (x^2*y^2), [x, -2, 2], [y, -2, 2],
[grid, 29, 29],
[palette, get_plot_option(palette,5)])$
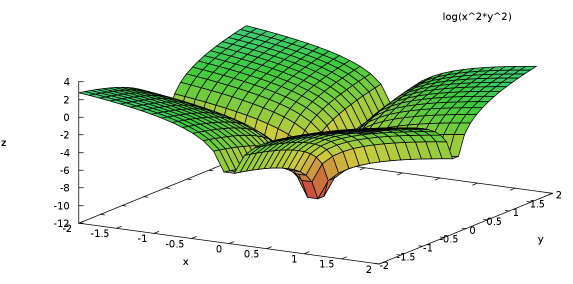
SymPy aims to be a lightweight normal Python module so as to become a nice open source alternative to Maple/Mathematica. Its goal is to be reasonably fast, easily extended with your own ideas, be callable from Python and could be used in real world problems. SymPy is perfectly multiplatform, it's small and easy to install and use, since it is written in pure Python (and doesn't need anything else).
You can choose to use either SymPy or Maxima, depending on what your needs are. For more information you can go to the official sites of SymPy and Maxima.