-
Notifications
You must be signed in to change notification settings - Fork 0
UD series definitions
In order to clarify the discussions about Taylor series and asymptotic expansions, it is necessary to define the relevant concepts as precisely as possible.
Sympy makes a sharp distinction between expressions and functions. In the following, whenever something is defined for a function (f), there's an equivalent definition applying to the expression (f(x)).
In this section we attract attention to the structure of finite or infinite series.
The term formal which is used below for series usually means that "Historically, mathematicians such as Leonhard Euler operated liberally with infinite series, even if they were not convergent. When calculus was put on a sound and correct foundation in the nineteenth century, rigorous proofs of the convergence of series were always required. However, the formal operation with non-convergent series has been retained in rings of formal power series which are studied in abstract algebra." In other words, operations with formal series depend only upon the coefficients, the basis, not upon (X) itself, so (X) is a formal parameter. ( They can be depend of (X) nature: complex, real and so on.)
A Series is the sum of the terms of a sequence. Finite sequences and series have defined first and last terms, whereas infinite sequences and series continue indefinitely. The terms of the series are often produced according to a certain rule, such as by a formula, or by an algorithm. Remark about context: When talking about series, one can refer either to the sequence (S_N) of the partial sums, or to the result - the sum of the series.
A formal power series is an object of the form (S = \sum_{n=0}^{+\infty} a_n X^n) where (X) is a formal parameter. The set of formal power series over a field (K) is noted (KX) and has a ring structure.
A classical Laurent series is an object of the form (\sum_{n=-\infty}^{+\infty} a_n X^n).
A generalized formal power series, or formal Laurent series, is an object (S) such that (X^n S) is a formal power series for some integer (n). The set of formal Laurent series over a field (K) is noted (K((X))) and has a field structure.
A Laurent polynomial in one variable over a field (F) is a linear combination of positive and negative powers of the variable with coefficients in (F). Laurent polynomials in (X) form a ring denoted (F [X, X−1] ). They differ from ordinary polynomials in that they may have terms of negative degree. A Laurent polynomial over C may be viewed as a Laurent series in which only finitely many coefficients are non-zero.
The Taylor series at (x_0) of a smooth function (f) is the formal power series (TS_{x_0}(f) = \sum_{n = 0}^\infty \frac{f^{(n)}(x_0)}{n!} X^n). where (X = x-x_0) (f) is analytic iff there exists a neighbourhood (V) of (x_0) where (f(x) = S(x-x_0), x \in V, S = TS_{x_0}(f)).
The n-th order Taylor polynomial of f at (x_0) is the degree-n polynomial (TP_{n, x_0}(f) = \sum_{n = 0}^n \frac{f^{(k)}(x_0)}{k!} X^k). If f is analytic, (TP_{n, x_0}(f)) is the degree-n truncation of (TS_{x_0}(f)).
A generalised power series, as used by the gruntz algorithm for computing limits, is an expression of the form (\sum_{n > 0} a_n x^{b_n}). Here the numbers (b_n) may be any complex numbers, but their real parts must be increasing: (Re(b_1) < Re(b_2) < \dots). The (a_n) are elements of the logarithmic closure of (\mathbb{C}(log(x))), that is finite expressions involving complex numbers, field operations, the function log, and the symbol log(x). Any laurent series with finite principal part is such a generalised power series.
These are all of the generalised power series type:
( \sqrt{\sin(x)} = x^{\frac{1}{2}} - \frac{x^{\frac{5}{2}}}{12} + \frac{x^{\frac{9}{2}}}{1440} + \cdots )
( x^x = 1 + x \log x + \frac{x^2 \log^2(x)}{2} + \cdots )
This series do not expand to Taylor series because of they are not analytical (some derivatives are oo)
Also combination of that function with each other or with polynomials brings to mix of various kinds of series (that may be out of sense).
Another question is whether appropriate asymptotic expansion for this series exists (especially for second series) with term Big-O: there is no constant ( C) such that ( C (x \log x) < 1 ) while ( x \rightarrow 0 ).
Nevertheless, the second series can be formalized as power series, but with formal variable ( Х = x \log x ). And the first one as power series with multiplication of it by some factor ( x^{\frac{1}{2}} ).
In this section we attract attention to the asymptotic expansion and related things.
f is dominated by g at (x_0), written (f = O_{x_0}(g)), if (f/g) is bounded at (x_0). Similarly, (f(x) = O_{x \rightarrow x_0}(g(x))) if (f = O_{x_0}(g)), i.e. if (f(x)/g(x)) is bounded for (x) going to (x_0). Note that (\cdot = O_\cdot(\cdot)) is a purely notational device here, not an equality.
The set of functions dominated by a function (g) at (x_0), (O_{x_0}(g)) is defined by (f \in O_{x_0}(g)) if (f = O_{x_0}(g)). (h + O(g)) is a set of functions defined in the usual way: (h + O(g) = {h+\alpha ; \alpha \in O(g)}). It is called an asymptotic expansion of f if (f \in h + O(g)).
Asymptotic series, otherwise asymptotic expansions, are infinite series whose partial sums become good approximations in the limit of some point of the domain (to a given function as the argument of the function tends towards a particular, often infinite, point). In general they do not converge.
The n-th order Taylor expansion of f at (x_0) is (TP_{n, x_0}(f)(x-x_0) + O_{x \rightarrow x_0}((x-x_0)^{n+1}))
This section is not really related with expansion but related with series. Roughly speaking, it is inversion of asymptotic series goals: while we have infinite number of coefficients of series then we obtain some function which is generated by them.
"However such interpretation is not required to be possible, because formal power series are not required to give a convergent series when a nonzero numeric value is substituted for x. Also, not all expressions that are meaningful as functions of x are meaningful as expressions designating formal power series; negative and fractional powers of x are examples of this. Generating functions are not functions in the formal sense of a mapping from a domain to a codomain; the name is merely traditional, and they are sometimes more correctly called generating series."
The ordinary generating function of a sequence (a_n) is ( G(a_n;x) = \sum_{n=0}^{+\infty} a_n x^n).
The exponential generating function of a sequence (a_n) is ( EG(a_n;x) = \sum_{n=0}^{+\infty} a_n \frac{x^n}{n!}).
In mathematics, an analytic function is a function that is locally given by a convergent power series. (There exist both real analytic functions and complex analytic functions .) Alternatively, an analytic function is an infinitely differentiable function such that the Taylor series at any point x0 in its domain converges to ƒ(x) for x in a neighborhood of x0.
Properties
- The sums, products, and compositions of analytic functions are analytic.
- The reciprocal of an analytic function that is nowhere zero is analytic, as is the inverse of an invertible analytic function whose derivative is nowhere zero.
- Any analytic function is smooth, that is, infinitely differentiable. The converse is not true; in fact, in a certain sense, the analytic functions are sparse compared to all infinitely differentiable functions.
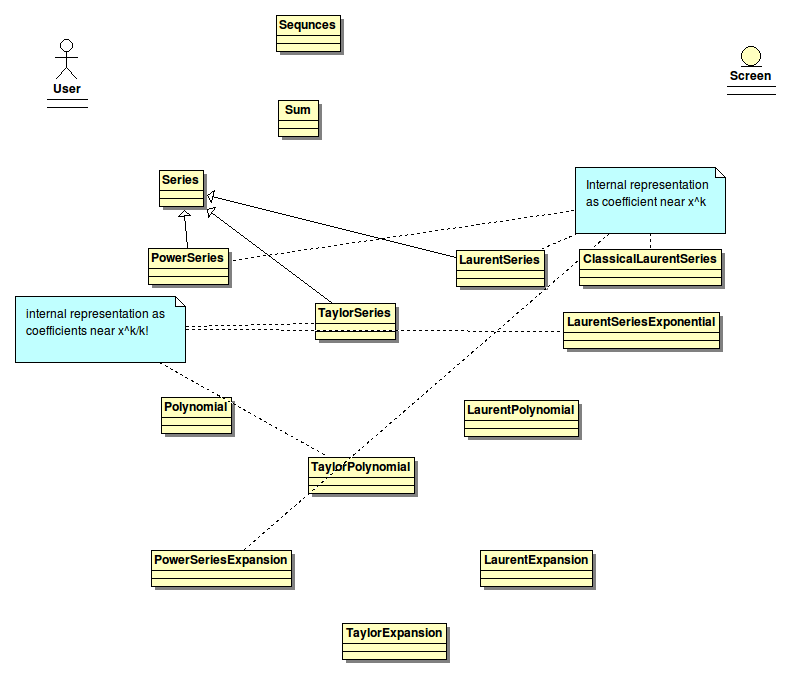
Al of the above it mathematical (historical) definitions.
In this section we try to classify them closer to programming.
By matter:
- Series - infinte number of powers
- Expansion - finite number of powers, with O
- Polynome - finite number of powers
By range:
- non negative powers (infinite or finite) (PowerSeries, TaylorSeries)
- finite negative and (infinite or finite) positive powers (LaurentSeries)
- infinite negative and (infinite or finite) positive power (ClassicalLaurentSeries)
By internal representation:
- coefficients near x^k (PowerSeries, GeneratingFunction)
- coefficients near x^k/k! (TaylorSeries, GeneratingFunctionExponential)
- coefficients near some expression f.e. (x*log x)^k powers.
- coefficients near x^k and multiplpication of series by some expression
Image: