Kratos For Dummies: Transient non linear heat transfer

Overview

In this second part we will modify the element and the solver in order to compute a transient non-linear problem, in other words, compute the dynamic contribution of the element. We will use the tools already available on the Kratos framework (or KratosCore), like the Newton-Rahpson strategy, the convergence criterion and the BDF scheme.

In order to accommodate the interoperability with other applicatiion in Kratos we will show how to integrate the already developed solver into the common interface for all the solvers. Finally all this will be integrated in one analysis stage file, that will replace the main script file. Helping in the future the development of coupled solver.

With all this components we will be able to run our problem in the same way it is designed and planned to be in the standard GiD interface. This will help you to integrate your developments into the Kratos ecosystem.

Additionally, you can see all the tools, processes, classes, variables, etc... available on the pỳthon interface of the KratosCore here.

Contents

1. Adding dynamic contribution to the element
   1. "Mass" matrix
   2. "Damping" matrix
2. Updating solver to Non-linear and transient
   1. Adapt our solver to the common solver interface
   2. Creating a wrapper of convergence criterion
   3. Adding the transient scheme
   4. Using the Newton-Rahpson strategy
3. Integrate into an analysis stage
4. Using *.json parameters

Adding dynamic contribution to the element

The equation to solve now will be:

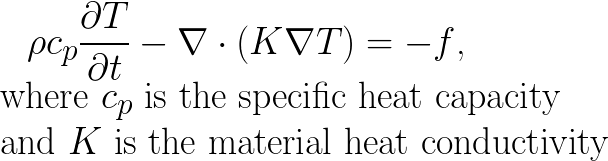
We have two different alternatives in order to compute the dynamic terms. Some elements compute internally the dynamic contribution. This is the case of the elements in the ConvectionDiffusionApplication and some fluid elements. The rest of the elements compute the contribution using mass and damping matrices (or the equivalent, depending of the physics being solved, the equivalent terms for the first and second time derivative).

Using the latter it is possible to use the interface of the existing schemes. The schemes are "utilities" used to compute the dynamic contributions of the problem. For this reason we will add the dynamic terms to our element.

In the following link the code to be added is presented: Tutorial: Adding dynamic contributions to the element file

Updating solver to Non-linear and transient

We will modify our solver in order to enhance the capabilities, making us possible to compute a non-linear transient problem.

Adapt our solver to the common solver interface

The base python interface can be found in Kratos/kratos/python_scripts/python_solver.py. Respect the previous script the following adds:

• We use the VariableUtils which provide a performance boost in some operations.

In the following link the complete proposed script can be found.

Tutorial: Pure diffusion solver derived from main python solver

Creating a wrapper of convergence criteria

The following wrapper for the convergence criteria is already available in the Kratos/kratos/python_scripts/base_convergence_criteria_factory.py. Like we are not considering any additional convergence criteria to the ones available on the framework we can work taking into account just these.

The detail of this implementation can be follow in the Tutorial: Creating a wrapper of convergence criteria

Adding the transient scheme

Depending of the approach followed on the implementation of our element

Using the Newton-Rahpson strategy

Finally, with all these components we are ready to integrate them into

Integrate into an analysis stage

This is a crucial step in order to achieve the proper integration of you code with the other applications and reach the objective of integrate your problem and create a multi-physics simulation.

Tutorial: Analysis stage for pure diffusion problem

Using *.json parameters

Once everything has been packed into the designed workflow, using analysis and solvers derived from the already existing scripts and classes, we can define our problem using directly the a pair of *.json files, one for the configuration parameters and another for the material properties. In the following we will need to modify these files to modify our problem. Of course for more options we can always develop our own processes.

Now our main python script will contain only the following:

from __future__ import print_function, absolute_import, division #makes KratosMultiphysics backward compatible with python 2.6 and 2.7

import KratosMultiphysics
import KratosMultiphysics.MyLaplacianApplication as Poisson

from poisson_analysis import PoissonAnalysis

"""
For user-scripting it is intended that a new class is derived
from PoissonAnalysis to do modifications
"""

if __name__ == "__main__":

    with open("ProjectParameters.json",'r') as parameter_file:
        parameters = KratosMultiphysics.Parameters(parameter_file.read())

    model = KratosMultiphysics.Model()
    simulation = PoissonAnalysis(model,parameters)
    simulation.Run()