Tree
Author: Dion, Ever
트리는 응용 분야가 굉장히 다양한 자료구조입니다.
어떤 트리는 조직도 같이 계층적인 데이터를 표현하는데 사용되고, 어떤 트리는 수식을 표현할 때 사용됩니다.
또 어떤 트리는 집합을 나타내는데 사용되며, 심지어는 데이터의 탐색을 위한 트리도 있습니다.
트리의 가장 중요한 응용 분야 중 하나는 탐색인데, 탐색 트리는 공부할 것도 많고 탐색 알고리즘을 이해해야 하기 때문에 어렵다고 볼 수 있습니다.
배열이나 연결리스트는 데이터를 일렬로 저장하기 때문에 탐색 연산이 순차적으로 수행되어야 한다는 단점을 가진다. 배열은 미리 정렬해 놓으면 이진탐색을 통해 효율적인 탐색이 가능하지만, 삽입이나 삭제 후에도 정렬 상태를 유지해야 하므로 삽입이나 삭제하는데 O(N) 시간이 소요된다. 이러한 문제점을 보완한 계층적(Hierarchical) 자료 구조가 트리(Tree)이다.
트리(Tree)는 나무를 닮은 자료구조라고 하지만, 정확히는 뿌리를 중심으로 뻗어나오는 그 구조를 닮았습니다.
컴퓨터 과학에서 트리는 굉장히 활용도가 높은 자료구조입니다.
운영체제의 파일 시스템이 트리 구조로 이루어져 있고, HTML, XML을 다룰 때 사용하는 DOM(Document Object Model)도 트리 구조로 이루어져 있습니다.[그래서 DOM Tree라고 함]
검색 엔진이나, 데이터 베이스도 트리 자료구조에 기반해서 구현됩니다. (여기에 사용되는 트리 자료구조가 바로 탐색 트리라고 하는 것임.)
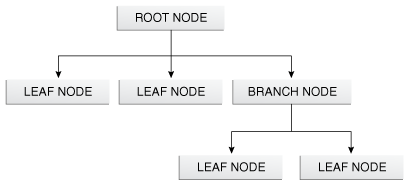
트리는 뿌리(Root), 가지(Branch), 잎(Leaf)의 세 가지 요소로 이루어져 있습니다.
뿌리, 가지, 잎 모두가 똑같은 Node라는 것을 염두에 둬야합니다. 이들은 그저 트리 내의 위치에 따라 명칭만 달라질 뿐입니다.
뿌리인 Root Node는 트리의 가장 위에 있는 Node를 가리키고 가지(Branch)는 뿌리와 잎 사이에 있는 모든 노드를 일컫는 말입니다.
그리고 가지의 끝에 매달려 있는 노드를 잎(Leaf)이라고 부릅니다. 끝에 있다고 해서 단말(Terminal) 노드라고 부르기도 합니다.
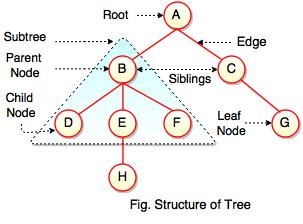
B에서 D, E, F가 나오게 되는데 B를 D, E, F의 부모(Parent)라고 부르고, D, E, F를 자식(Child, Children)이라고 부릅니다.
B와 C는 같은 부모(A)를 가진 형제(Sibling)라고 부릅니다.
B와 G는 아무런 관계를 가지고 있지 않습니다.
- 루트(Root) 노드 : 트리의 최상위에 있는 노드
- 부모(Parent) 노드 : 노드 상위에 연결된 노드
- 자식(Child) 노드 : 노드 하위에 연결된 노드
- 형제(Sibling) 노드 : 동일한 부모를 가지는 노드
- 조상(Ancestor) 노드 : 루트 노드까지의 경로상에 있는 모든 노드들의 집합
- 후손(Descendant) 노드 : 노드 아래로 매달린 모든 노드들의 집합
- 서브트리(Subtree) : 노드 자신과 후손 노드로 구성된 트리
- 차수(Degree) : 자식 노드 수
- 레벨(Level) : 루트 노드가 레벨 1에 있고 아래로 내려가며 레벨이 1씩 증가한다. 레벨은 깊이(Depth)와 같다
- 높이(Height) : 트리의 최대 레벨
- 키(Key) : 탐색에 사용되는 노드에 저장된 정보
- 이파리(Leaf) 노드 : 자식이 없는 노드, 단말(Terminal) 노드 또는 외부(External) 노드라고도 한다. 이파리가 아닌 노드를 비 단말(Non-Terminal) 노드 또는 내부(Internal) 노드라고 한다
일반적인 트리를 메모리에 저장하려면 각 노드에 키와 자식 수만큼의 레퍼런스를 저장해야 한다. 따라서 트리 노드의 최대 차수가 k라면, k+1개의 레퍼런스 필드를 선언해야 한다.
최대 차수가 k인 트리에 N개의 노드가 있다면, null 레퍼런스 수는 Nk - (N-1) = N(k-1) + 1 이다. 여기서 Nk는 총 레퍼런스 수이고, N-1은 트리에서 실제 부모 자식을 연결하는 레퍼런스 수이다.
- 이파리노드도 k개의 레퍼런스를 가지고 있다.
- 2개의 노드를 연결하기 위해선 1개의 선이 필요하고, N개의 노드를 연결하기 위해선
N-1개의 선이 필요하다
따라서 k가 클수록 메모리의 낭비가 심해지는 것은 물론 트리를 탐색하는 과정에서 null 레퍼런스를 확인해야 하므로 시간적으로도 매우 비효율적이다.
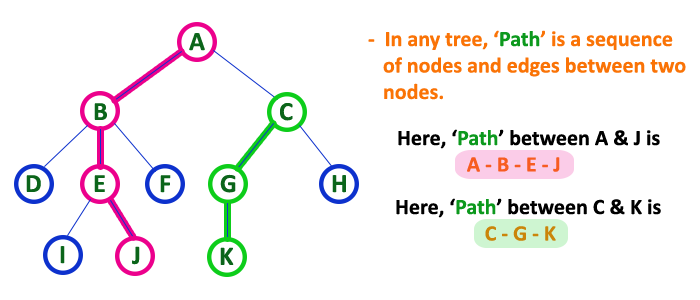
트리에서 경로는 한 노드에서부터 다른 한 노드까지 이르는 길 사이에 놓여있는 순서입니다.
예를 들어서 A노드에서 J노드까지 이른다면 A노드에서 출발하여, B노드를 거치고, E노드를 거친다음 J노드에 도착하게 됩니다.
이 때 "A-B-E-J"를 A에서 J까지의 경로라고 합니다. (Path between A & J)
경로는 길이(Length)라는 속성을 가지는데, 출발하는 노드에서 목적지 노드까지 거쳐야하는 노드의 개수를 얘기합니다.
이 때, 출발하는 노드는 포함하지 않기 때문에 A에서 J까지의 경로는 3의 길이를 가집니다.
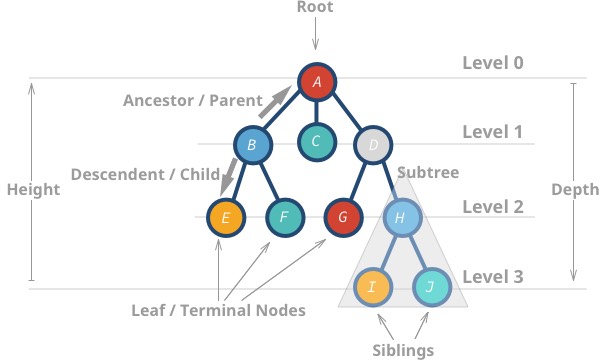
노드의 깊이(Depth)는 루트 노드에서 해당 노드까지의 경로의 길이를 뜻합니다.
A에서 H까지의 경로가 "A-D-H" 이므로 경로의 길이는 2입니다. 따라서 깊이는 2입니다.
그렇다면, 루트의 깊이는 얼마일까요? 0입니다.
깊이와 비슷한 개념의 용어로 레벨(Level)과 높이(Height)가 있습니다. 비슷한 것입니다. 같은 것이 아닙니다.
레벨은 깊이가 같은 노드의 집합을 일컫는 말입니다.
트리의 높이는 '가장 깊은 곳'에 있는 잎 노드까지의 깊이를 뜻합니다. 그럼 위 그림에 있는 트리의 높이는 얼마일까요?
3입니다.
마지막으로 설명할 개념은 차수(Degree)입니다. 노드의 차수라함은 그 노드의 자식 노드 개수를 말하는 것이고, 트리의 차수라함은 트리 내에 있는 노드들 가운데 자식 노드가 가장 많은 노드의 차수를 말하는 것입니다.
위의 그림에서는 A노드의 차수는 3이고, B 노드의 차수는 2입니다. 트리 전체적으로 보면 자식이 가장 많은 노드는 A이므로 위 트리의 차수는 3입니다.
트리는 여러가지 방법으로 표현이 가능합니다. 거꾸로 된 나무 그림이 대표적이지만, 그 외에도 여러 방법들이 사용됩니다.
같은 레벨의 노드들을 괄호로 같이 묶어 표현하는 방법입니다.
읽기는 다소 어렵지만, 트리를 하나의 공식처럼 표현할 수 있는 장점이 있습니다.
트리가 하위 트리의 집합이라는 관계를 잘 표현할 수 있음
마지막으로 트리는 들여쓰기 (Indentation)로도 표현이 가능합니다.
들여쓰기 표현법은 자료의 계층적인 특징을 잘 나타냅니다.
노드의 표현은 부모와 자식, 그리고 형제 노드를 서로 연결짓는 방법입니다.
트리 노드를 표현하는 방법에는 두 가지가 있습니다. 하나는 'N-링크(N-Link)' 표현법이고, 다른 하나는 '왼쪽 자식-오른쪽 형제(Left Child-Right Sibling)' 표현법입니다.
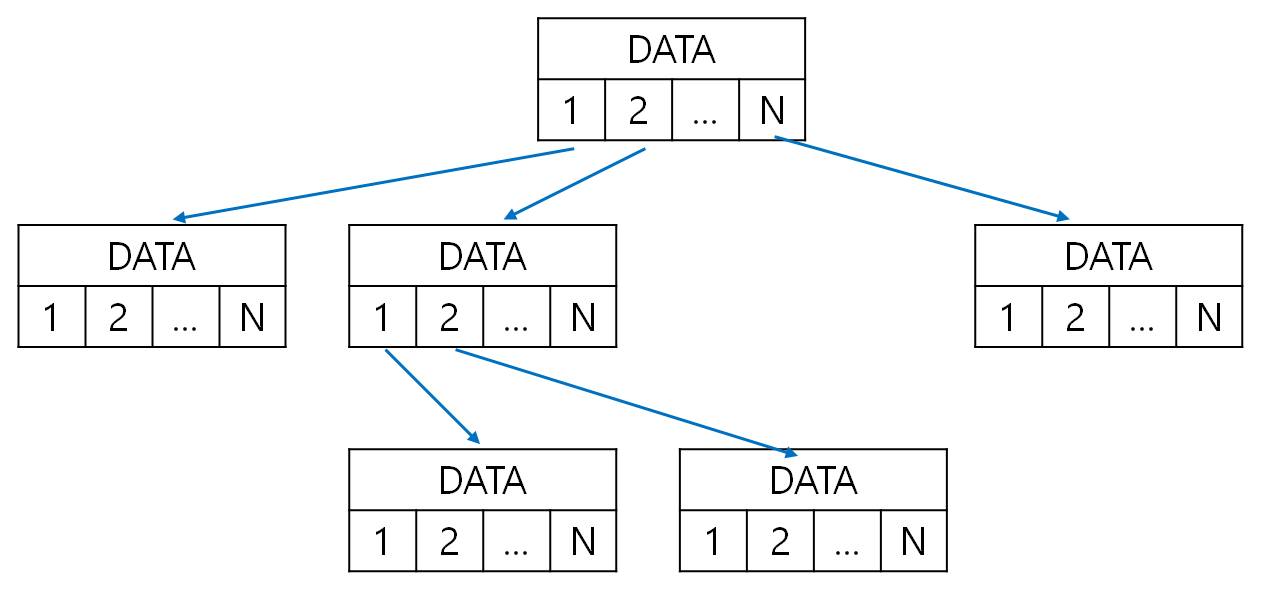
N-Link는 노드의 차수가 N이라면, 노드가 N개의 링크를 가지고 있어서 이 링크들이 각각 자식 노드를 가리키도록 노드를 구성하는 방법입니다.
이 노드로 트리를 이룬다면 트리는 다음과 같은 모습이 됩니다.
이 표현법은 언뜻 봤을 때에는 쓸만해 보이지만, 차수(Degree)가 노드마다 달라지는 트리에는 적용하기가 어려운 단점이 있습니다.
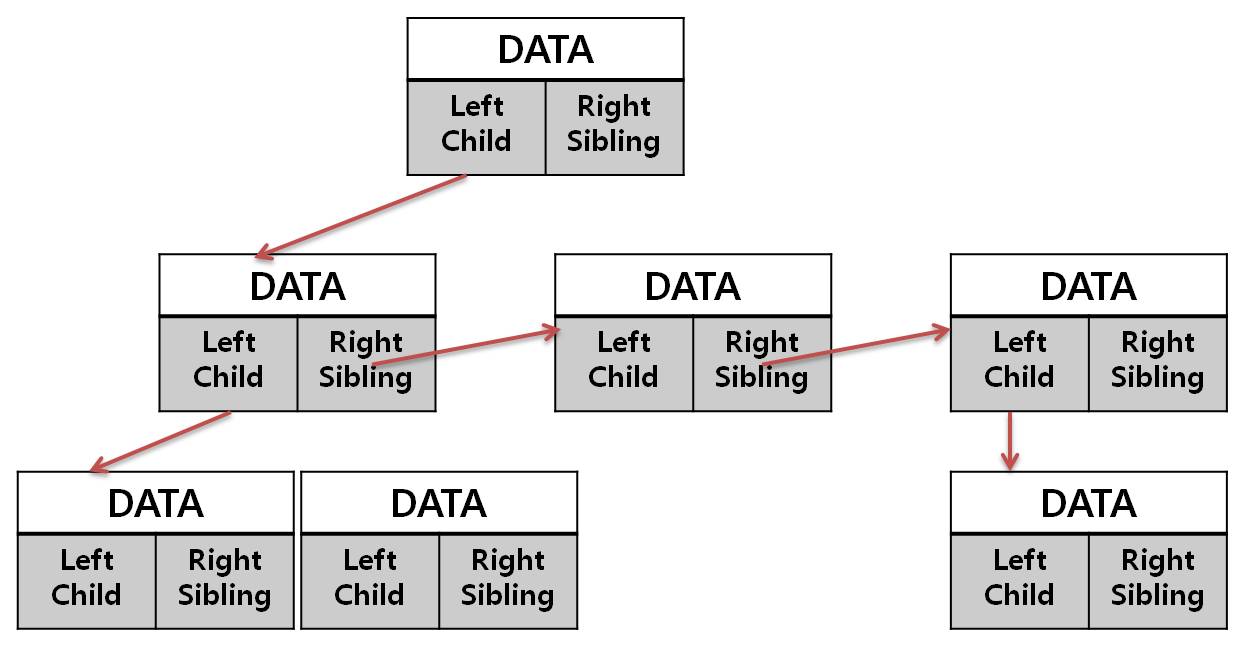
위의 문제를 해결하기 위한 표현법입니다. 이 방법을 사용하면 N개의 차수를 가진 노드의 표현이 두 개의 포인터, 왼쪽 자식-오른쪽 형제만으로 가능하게 됩니다.
이 표현법을 사용하는 트리에서 어느 한 노드의 모든 자식 노드를 얻으려면 왼쪽 자식 노드에 대한 포인터만 있으면 됩니다.
이 포인터를 이용해서 왼쪽 자식 노드의 주소를 얻고, 또 그 다음 오른쪽 형제 노드의 주소를 계속해서 얻어 나가면 결국에는 모든 자식 노드를 얻을 수 있습니다.
LCRS는 노드의 차수가 일정하지 않은 일반적인 트리를 구현하는 매우 효율적인 자료구조이다.
뇌를 자극하는 알고리즘
http://www.btechsmartclass.com/data_structures/tree-terminology.html
https://adrianmejia.com/data-structures-for-beginners-trees-binary-search-tree-tutorial/
https://en.wikipedia.org/wiki/Nested_set_model
소감
Dion
다 하고 적기
Ever
다 하고 적기
Hamill
다 하고 적기
Lynn
다 하고 적기
Sunny
다 하고 적기