generated from cotes2020/chirpy-starter
-
Notifications
You must be signed in to change notification settings - Fork 0
Commit
This commit does not belong to any branch on this repository, and may belong to a fork outside of the repository.
- Loading branch information
1 parent
f80d4d9
commit a643701
Showing
3 changed files
with
867 additions
and
0 deletions.
There are no files selected for viewing
This file contains bidirectional Unicode text that may be interpreted or compiled differently than what appears below. To review, open the file in an editor that reveals hidden Unicode characters.
Learn more about bidirectional Unicode characters
| Original file line number | Diff line number | Diff line change |
|---|---|---|
| @@ -0,0 +1,312 @@ | ||
| --- | ||
| layout: post | ||
| title: Robotics 4 - Kinematics | ||
| author: wichai | ||
| date: 2024-11-13 9:00 | ||
| categories: [Study, Master] | ||
| tags: [DU, Robotics] | ||
| mermaid: true | ||
| math: true | ||
| pin: false | ||
| --- | ||
|
|
||
| From @VergilOP | ||
|
|
||
| ## Lecture 4 - Kinematics | ||
|
|
||
| ### Learning Objectives | ||
|
|
||
| Objectives: | ||
|
|
||
| 1. Spatial Description | ||
| 2. Transformation | ||
|
|
||
| - Rotation | ||
| - Translation | ||
|
|
||
| ### Spatial Description 空间描述 | ||
|
|
||
| - Position of a Point 点的位置 | ||
| - With respect to a fixed origin O, the position of a point P is described by the vector OP(p) | ||
| 相对于固定原点 O,点 P 的位置由向量 OP(p) 描述 | ||
|
|
||
| - Coordinate Frames: | ||
| - Rotation | ||
| - Translation | ||
|
|
||
| - Rigid body configuration: | ||
| - Position: $^AP$ | ||
| - Orientation: $\{^AX_B, ^AY_B, ^AZ_B\}$ | ||
|
|
||
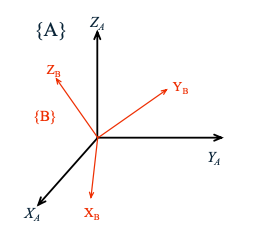
| > These vectors describe rotation of {B} with respect to {A} | ||
| <img src="https://wichaiblog-1316355194.cos.ap-hongkong.myqcloud.com/image-20241128181058807.png" alt="image-20241128181058807" /> | ||
|
|
||
| ### Transformation | ||
|
|
||
| #### Rotation | ||
|
|
||
|  | ||
|
|
||
| - **Rotation Matrix:** | ||
|
|
||
| **旋转矩阵(Rotation Matrix)**用于描述坐标系之间的旋转关系。假设有两个坐标系${A}$和${B}$,旋转矩阵$^A_BR$表示从坐标系${B}$到坐标系${A}$的旋转。 | ||
| $$ | ||
| ^A_BR | ||
| = \begin{bmatrix} | ||
| r_{11} & r_{12} & r_{13} \\ | ||
| r_{21} & r_{22} & r_{23} \\ | ||
| r_{31} & r_{32} & r_{33} | ||
| \end{bmatrix} | ||
| = \begin{bmatrix} ^A \hat{X}_B & ^A \hat{Y}_B & ^A \hat{Z}_B \end{bmatrix} | ||
| = \begin{bmatrix} {^B \hat{X}_A}^T \\ {^B \hat{Y}_A}^T \\ {^B \hat{Z}_A}^T \end{bmatrix} = {^B_A R}^T | ||
| = \begin{bmatrix} | ||
| \hat{X}_B \cdot \hat{X}_A & \hat{Y}_B \cdot \hat{X}_A & \hat{Z}_B \cdot \hat{X}_A\\ | ||
| \hat{X}_B \cdot \hat{Y}_A & \hat{Y}_B \cdot \hat{Y}_A & \hat{Z}_B \cdot \hat{Y}_A\\ | ||
| \hat{X}_B \cdot \hat{Z}_A & \hat{Y}_B \cdot \hat{Z}_A & \hat{Z}_B \cdot \hat{Z}_A | ||
| \end{bmatrix} | ||
| $$ | ||
|
|
||
| 表达式 基向量组合形式 转置形式 点积形式 | ||
|
|
||
| $^B \hat{X}_A$表示在坐标系${B}$中,坐标系${A}$的X轴单位向量。同理,其他项以此类推。 | ||
|
|
||
| $\hat{X}_B$、$\hat{Y}_B$、$\hat{Z}_B$是坐标系${B}$的单位基向量,$\hat{X}_A$、$\hat{Y}_A$、$\hat{Z}_A$是坐标系${A}$的单位基向量。 | ||
|
|
||
|
|
||
|
|
||
| 旋转矩阵是一个**正交矩阵(Orthogonal Matrix)**,其转置等于其逆矩阵。 | ||
|
|
||
| > - Inverse of Rotation Matrix(Orthonormal Matrix) | ||
| > $$ | ||
| > ^A_BR^{-1} =\ ^B_AR =\ ^A_BR^T | ||
| > $$ | ||
| - State description: $^A\hat{X}_B = ^A_BR\ \ ^B\hat{X}_B$ | ||
|
|
||
| $$ | ||
| ^A \hat{X}_B = {^A_B R} \begin{bmatrix} 1 \\ 0 \\ 0 \end{bmatrix}\\ | ||
| ^A \hat{Y}_B = {^A_B R} \begin{bmatrix} 0 \\ 1 \\ 0 \end{bmatrix}\\ | ||
| ^A \hat{Z}_B = {^A_B R} \begin{bmatrix} 0 \\ 0 \\ 1 \end{bmatrix} | ||
| $$ | ||
|
|
||
| - Dot product: 通过点积,可以计算基向量在不同坐标系中的投影关系。 | ||
| $$ | ||
| ^A \hat{X}_B | ||
| = \begin{bmatrix} \hat{X}_B \cdot \hat{X}_A \\ \hat{X}_B \cdot \hat{Y}_A \\ \hat{X}_B \cdot \hat{Z}_A \end{bmatrix}\\ | ||
| ^A \hat{Y}_B | ||
| = \begin{bmatrix} \hat{Y}_B \cdot \hat{X}_A \\ \hat{Y}_B \cdot \hat{Y}_A \\ \hat{Y}_B \cdot \hat{Z}_A \end{bmatrix}\\ | ||
| ^A \hat{Z}_B | ||
| = \begin{bmatrix} \hat{Z}_B \cdot \hat{X}_A \\ \hat{Z}_B \cdot \hat{Y}_A \\ \hat{Z}_B \cdot \hat{Z}_A \end{bmatrix} | ||
| $$ | ||
| 其中,每个元素表示${B}$的基向量在${A}$的基向量方向上的投影。例如,$\hat{X}_B \cdot \hat{X}_A$表示${B}$的X轴在${A}$的X轴方向上的投影。 | ||
|
|
||
| - Description of a Frame: | ||
|
|
||
| - **描述一个坐标系需要知道其基向量和原点位置**: | ||
| - 坐标系${B}$在${A}$中的表示包括: | ||
| - 基向量:$^A \hat{X}_B$、$^A \hat{Y}_B$、$^A \hat{Z}_B$ | ||
| - 原点位置:$^A P_{B_{\text{org}}}$ | ||
| - Frame{B}: $^A \hat{X}_B, ^A \hat{Y}_B, ^A \hat{Z}_B$, $^AP_{Borg}$ | ||
| - 这里,$^A_BR$是从${B}$到${A}$的旋转矩阵,$^A P_{B_{\text{org}}}$是${B}$的原点在${A}$坐标系中的位置向量。 | ||
|
|
||
|
|
||
| $$ | ||
| \{B\} = \{^A_BR\space\space^AP_{Borg}\} | ||
| $$ | ||
|
|
||
| - Mapping: | ||
|
|
||
| - Changing descriptions from frame to frame | ||
| - **映射**是指将一个向量从一个坐标系转换到另一个坐标系。 | ||
| - **旋转变换**: | ||
| - 当我们知道向量在${B}$坐标系中的表示$^B P$,想要得到它在${A}$坐标系中的表示$^A P$,可以使用旋转矩阵进行变换。 | ||
|
|
||
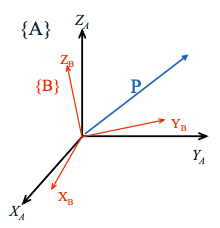
| - Rotations | ||
|  | ||
|
|
||
| - 假设有一个向量$P$,它在坐标系${B}$中的表示为$^B P$。我们想要计算它在坐标系${A}$中的表示$^A P$。 | ||
| - 首先,利用${B}$和${A}$的基向量之间的关系: | ||
| - If $P$ is in $\{B\}$: $^BP$ | ||
|
|
||
| $$ | ||
| ^AP = \begin{bmatrix} | ||
| ^B \hat{X}_A. ^BP \\ ^B \hat{Y}_A. ^BP \\ ^B \hat{Z}_A. ^BP | ||
| \end{bmatrix} | ||
| = \begin{bmatrix} | ||
| ^B \hat{X}_A^T \\ ^B \hat{Y}_A^T \\ ^B \hat{Z}_A^T | ||
| \end{bmatrix} | ||
| \cdot\ ^BP | ||
| $$ | ||
|
|
||
| $$ | ||
| ^AP =\ ^A_BR\ ^BP | ||
| $$ | ||
| - 这意味着,可以直接使用旋转矩阵$^A_BR$将向量从${B}$坐标系转换到${A}$坐标系。 | ||
|
|
||
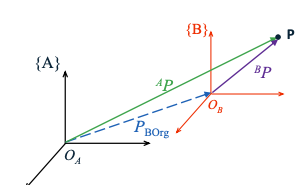
| #### Translation 平移 | ||
|
|
||
|  | ||
|
|
||
| $$ | ||
| ^AP_{OA} = ^AP_{OB} + ^AP_{BOrg} | ||
| $$ | ||
|
|
||
|
|
||
|
|
||
| #### General Transformation | ||
|
|
||
| #### <img src="https://wichaiblog-1316355194.cos.ap-hongkong.myqcloud.com/image-20241129103914524.png" alt="image-20241129103914524" style="zoom:50%;" /> | ||
|
|
||
| $$ | ||
| ^AP =\ ^A_BR\ ^BP +\ ^AP_{Borg} \\ | ||
| \begin{bmatrix} | ||
| ^AP \\ | ||
| 1 | ||
| \end{bmatrix} | ||
| = \begin{bmatrix} | ||
| ^A_BR &\ ^AP_{Borg} \\ | ||
| 0\ 0\ 0 & 1 | ||
| \end{bmatrix} | ||
| = \begin{bmatrix} | ||
| ^BP\\ | ||
| 1 | ||
| \end{bmatrix} | ||
| $$ | ||
|
|
||
| $^A P$:点$P$在坐标系${A}$中的表示。 | ||
|
|
||
| $^B P$:点$P$在坐标系${B}$中的表示。 | ||
|
|
||
| $^A_B R$:从${B}$到${A}$的旋转矩阵。 | ||
|
|
||
| $^A P_{B_{\text{org}}}$:坐标系${B}$的原点在${A}$中的位置。 | ||
|
|
||
|
|
||
|
|
||
| - Homogeneous Transformation: 齐次变换矩阵 | ||
|
|
||
| 统一旋转和平移 | ||
| $$ | ||
| ^AP_{(4\times1)} =\ ^A_BT_{(4\times4)}\ ^BP_{(4\times1)} | ||
| $$ | ||
|
|
||
| $^A_B T$是**齐次变换矩阵**,包括旋转和平移。 | ||
|
|
||
| - General Operators: | ||
| $$ | ||
| P_2 = | ||
| \begin{bmatrix} | ||
| R_k(\theta) & Q \\ | ||
| 0\ 0\ 0 & 1 | ||
| \end{bmatrix}P_1 | ||
| $$ | ||
|
|
||
| $$ | ||
| P_2 = T\ P_1 | ||
| $$ | ||
|
|
||
| $P_1$:初始点的齐次坐标表示。 | ||
|
|
||
| $P_2$:变换后的点的齐次坐标表示。 | ||
|
|
||
| $R_k(\theta)$:绕轴$k$旋转$\theta$角度的旋转矩阵。 | ||
|
|
||
| $Q$:平移向量。 | ||
|
|
||
| - Inverse Transform 逆变换 | ||
| $$ | ||
| ^A_B T = \begin{bmatrix} | ||
| ^A_B R & ^A P_{Borg} \\ | ||
| 0\ 0\ 0 & 1 \end{bmatrix} | ||
| $$ | ||
|
|
||
| $$ | ||
| ^A_B T^{-1} = ^B_A T = | ||
| \begin{bmatrix} | ||
| ^A_B R^T & -^A_B R^T \cdot\ ^AP_{Borg} \\ | ||
| 0\ 0\ 0 & 1 \end{bmatrix} | ||
| $$ | ||
|
|
||
| - Homogeneous Transform Interpretations: | ||
|
|
||
| - Description of a frame 坐标系的描述 | ||
| 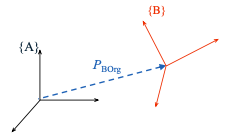 | ||
| $$ | ||
| ^A_BT:\{B\} = \{^A_BR\ \ ^AP_{Borg}\} | ||
| $$ | ||
|
|
||
| - Transform mapping 坐标的映射 | ||
| 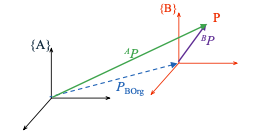 | ||
| $$ | ||
| ^A_BT:\ ^BP \rarr\ ^AP | ||
| $$ | ||
|
|
||
| - Transform operator 变换算子 | ||
| 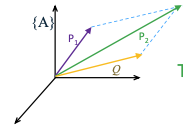 | ||
| $$ | ||
| T: P_1 \rarr P_2 | ||
| $$ | ||
| $P_1$:初始点。 | ||
|
|
||
| $P_2$:经过变换后的点。 | ||
|
|
||
| - Compound Transformation:复合变换 | ||
|
|
||
| <img src="https://wichaiblog-1316355194.cos.ap-hongkong.myqcloud.com/image-20241129105316388.png" alt="image-20241129105316388" style="zoom:50%;" /> | ||
| $$ | ||
| ^BP = ^B_C T \ C_P | ||
| $$ | ||
|
|
||
| $$ | ||
| ^AP = ^A_B T \ B_P | ||
| $$ | ||
|
|
||
| $$ | ||
| ^AP = ^A_B T \ ^B_C T \ C_P | ||
| $$ | ||
|
|
||
| $$ | ||
| ^A_C T = ^A_B T \ ^B_C T | ||
| $$ | ||
|
|
||
| $$ | ||
| ^A_C T = \begin{bmatrix} ^A_B R \ ^B_C R & ^A_B R \ ^B P_{Corg} + ^A P_{Borg} \\ 0\ 0\ 0 & 1 \end{bmatrix} | ||
| $$ | ||
|
|
||
| - Transform Equation | ||
|
|
||
| <img src="https://wichaiblog-1316355194.cos.ap-hongkong.myqcloud.com/image-20241129105332226.png" alt="image-20241129105332226" style="zoom:50%;" /> | ||
|
|
||
| - 在多个坐标系之间的循环变换中,变换矩阵的乘积应等于单位矩阵: | ||
|
|
||
| $$ | ||
| ^A_B T \ ^B_C T \ ^C_D T \ ^D_A T = I | ||
| $$ | ||
|
|
||
| #### Representations | ||
|
|
||
| - End-effector Configuration **末端执行器的齐次变换矩阵**: | ||
| 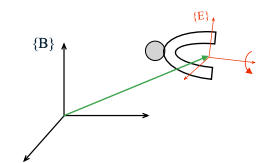 | ||
| $$ | ||
| ^B_ET: Position + Orientation | ||
| $$ | ||
| $^B_E T$表示末端执行器相对于基座坐标系${B}$的齐次变换矩阵,包含了位置和姿态的信息 | ||
|
|
||
| - End-effector configuration parameters: | ||
| $$ | ||
| X = \begin{bmatrix} | ||
| X_P \\ | ||
| X_R | ||
| \end{bmatrix} | ||
| $$ | ||
| $X_P$:位置参数,表示末端执行器在空间中的位置。 | ||
|
|
||
| **$X_R$**:姿态参数,表示末端执行器在空间中的方向或旋转。 | ||
|
|
||
| - Position representation: | ||
| 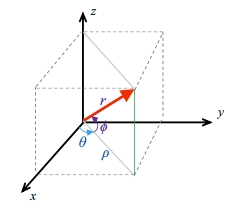 | ||
|
|
||
| - Cartesian: (x, y, z) 笛卡尔坐标系 | ||
| - Cylindrical: $(\rho, \theta, z)$ 圆柱坐标系 | ||
| - Spherical: $(r, \theta, \phi)$ 球坐标系 |
Oops, something went wrong.