Waveform Data Packet Descriptors Explained

The wording for the LAS full waveform fields can be confusing and historically has resulted in variable interpretations. This page attempts to add more clarity with some examples and imagery.

Waveform Data Storage

Full waveform (FWF) data in a LAS file has three relevant sources:

1. The Waveform Packet Descriptor stored in a VLR in the LAS header – This section describes how the FWF data is stored in the raw Waveform Data Packet (WDP), providing details like how many samples are in each packet, the temporal resolution (in picoseconds) of each sample, and the gain/offset values to convert raw values into numbers.
2. The Point Data Record of a particular point – The FWF-related Point Data Record Formats (PDRFs) contain fields that (a) describe the pulse vector from which a point was derived and (b) the location of that point's return on the pulse's FWF data. These attributes make it possible to translate a particular WDP sample into 3D space.
3. The Waveform Data Packet (WDP) itself – The WDP contains the waveform data itself for each pulse, which is simply a series of amplitudes collected over time for a particular pulse. The WDPs are almost always stored externally in a *.wdp file of the same name as the LAS file.

When interpreting the spatial location of a particular sample in the WDP, one must use the FWF parametric equation defined in the corresponding point record:

1. P_x = X_start + t * dx
2. P_y = Y_start + t * dy
3. P_z = Z_start + t * dz

The delta unit vector "<dx, dy, dz>" provides a means to compute the position "P_xyz" at a certain time "t" in picoseconds. The units of "dz, dy, and dz" should be the same spatial unit as the return's xyz coordinates, per picosecond.

Storage Size

For the sake of minimizing storage space, multiple returns from a given pulse can reference the same data packet. It is also possible to store a separate digitized waveform for each return, either by storing the exact same WDP multiple times or by storing only the section of the digitized waveform that is relevant for the corresponding return.

Finally, the actual storage size of the waveform data packet in its "Bits Per Sample" can be any number between 2 and 32, so long as the total packet size is rounded up to a full byte. More discussion on this question can be found here.

Standard Straight-Line Pulses

The delta vectors of all returns of one pulse remain constant if the laser light travels a straight line, which is a valid assumption for most topographic surveys. This illustration (Figure 1) gives a simple example of how three different returns of a laser pulse relate to their digitized waveform:

A few implications that may not be immediately obvious:

1. All three return points reference the same WDP because they are all from the same pulse.
2. The delta vector points toward the origin, not toward the returns. Thus, for airborne applications the "dz" will almost always be a positive value.
3. The FWF parametric equations are defined relative to an arbitrary Start Point "S", which is not necessarily one of the digitized returns. The location of "S" can be derived from of the three return points' Return Point Location and the FWF parametric equation. All three returns should give approximately the same XYZ coordinates for "S".
4. Coordinates derived from the parametric equations will be in reference to whatever units and coordinate system in which the parametric equations were originally derived - usually, when the LAS swaths were originally created. If the points have been subsequently reprojected or had their units changed, coordinates derived from the parametric equations may have unexpected results unless the parametric parameters were also updated for the new projection/units.

Refracted Pulses

In a bathymetric survey the laser beam may get refracted when it hits the water surface and change both direction and speed. By storing changes in the delta vector with each return it is possible to store the result of a refraction calculation to the LAS file as illustrated here (Figure 2):

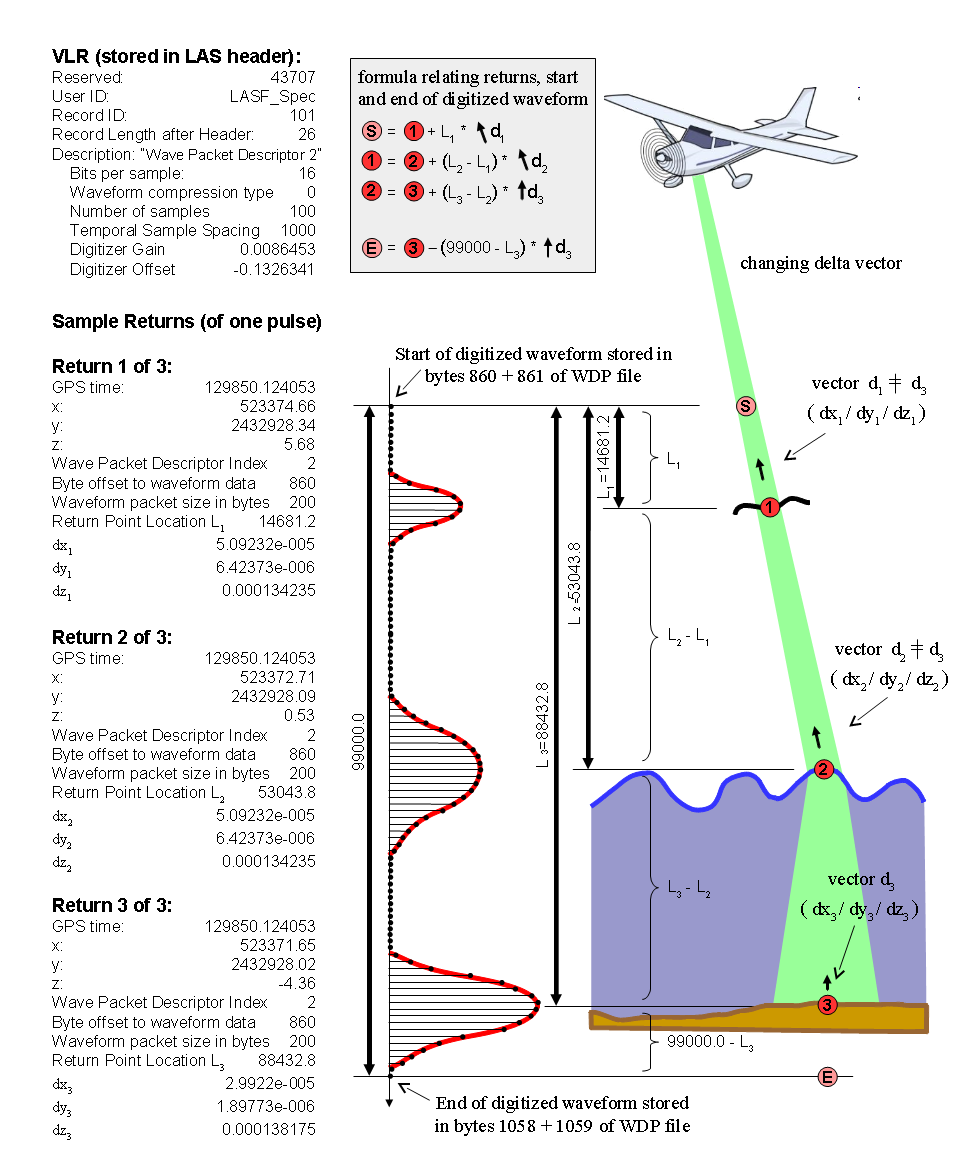
In this case the traversal of the digitized waveform needs to be done in segments:

• use the delta vector of the first return to traverse from the first return to the the start of the digitized waveform,
• use the delta vector of the second return to traverse from the second return to the first return,
• use the delta vector of the third return to traverse from the third return to the second return,
• ...
• use the delta vector of the last return to traverse from the last return to the second-to-last return or in reverse to the end of the digitized waveform.

Conclusion

That concludes the explanation of the FWF data.

Credit for the imagery goes to Martin Isenberg (@rapidlasso).