参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益!
给你一个大小为 m x n 的二进制矩阵 grid 。
岛屿 是由一些相邻的 1 (代表土地) 构成的组合,这里的「相邻」要求两个 1 必须在 水平或者竖直的四个方向上 相邻。你可以假设 grid 的四个边缘都被 0(代表水)包围着。
岛屿的面积是岛上值为 1 的单元格的数目。
计算并返回 grid 中最大的岛屿面积。如果没有岛屿,则返回面积为 0 。
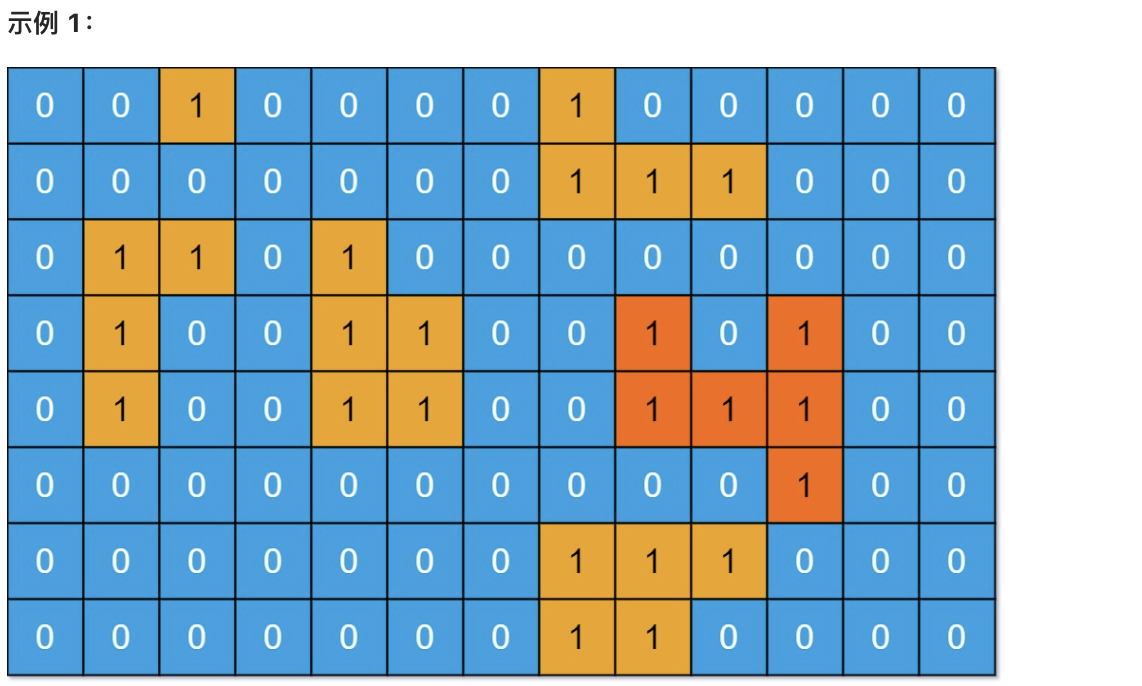
- 输入:grid = [[0,0,1,0,0,0,0,1,0,0,0,0,0],[0,0,0,0,0,0,0,1,1,1,0,0,0],[0,1,1,0,1,0,0,0,0,0,0,0,0],[0,1,0,0,1,1,0,0,1,0,1,0,0],[0,1,0,0,1,1,0,0,1,1,1,0,0],[0,0,0,0,0,0,0,0,0,0,1,0,0],[0,0,0,0,0,0,0,1,1,1,0,0,0],[0,0,0,0,0,0,0,1,1,0,0,0,0]]
- 输出:6
- 解释:答案不应该是 11 ,因为岛屿只能包含水平或垂直这四个方向上的 1 。
注意题目中每座岛屿只能由水平方向和/或竖直方向上相邻的陆地连接形成。
也就是说斜角度链接是不算了, 例如示例二,是三个岛屿,如图:
这道题目也是 dfs bfs基础类题目,就是搜索每个岛屿上“1”的数量,然后取一个最大的。
本题思路上比较简单,难点其实都是 dfs 和 bfs的理论基础,关于理论基础我在这里都有详细讲解 :
很多同学,写dfs其实也是凭感觉来,有的时候dfs函数中写终止条件才能过,有的时候 dfs函数不写终止添加也能过!
这里其实涉及到dfs的两种写法。
写法一,dfs只处理下一个节点,即在主函数遇到岛屿就计数为1,dfs处理接下来的相邻陆地
// 版本一
class Solution {
private:
int count;
int dir[4][2] = {0, 1, 1, 0, -1, 0, 0, -1}; // 四个方向
void dfs(vector<vector<int>>& grid, vector<vector<bool>>& visited, int x, int y) {
for (int i = 0; i < 4; i++) {
int nextx = x + dir[i][0];
int nexty = y + dir[i][1];
if (nextx < 0 || nextx >= grid.size() || nexty < 0 || nexty >= grid[0].size()) continue; // 越界了,直接跳过
if (!visited[nextx][nexty] && grid[nextx][nexty] == 1) { // 没有访问过的 同时 是陆地的
visited[nextx][nexty] = true;
count++;
dfs(grid, visited, nextx, nexty);
}
}
}
public:
int maxAreaOfIsland(vector<vector<int>>& grid) {
int n = grid.size(), m = grid[0].size();
vector<vector<bool>> visited = vector<vector<bool>>(n, vector<bool>(m, false));
int result = 0;
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
if (!visited[i][j] && grid[i][j] == 1) {
count = 1; // 因为dfs处理下一个节点,所以这里遇到陆地了就先计数,dfs处理接下来的相邻陆地
visited[i][j] = true;
dfs(grid, visited, i, j); // 将与其链接的陆地都标记上 true
result = max(result, count);
}
}
}
return result;
}
};写法二,dfs处理当前节点,即即在主函数遇到岛屿就计数为0,dfs处理接下来的全部陆地
dfs
// 版本二
class Solution {
private:
int count;
int dir[4][2] = {0, 1, 1, 0, -1, 0, 0, -1}; // 四个方向
void dfs(vector<vector<int>>& grid, vector<vector<bool>>& visited, int x, int y) {
if (visited[x][y] || grid[x][y] == 0) return; // 终止条件:访问过的节点 或者 遇到海水
visited[x][y] = true; // 标记访问过
count++;
for (int i = 0; i < 4; i++) {
int nextx = x + dir[i][0];
int nexty = y + dir[i][1];
if (nextx < 0 || nextx >= grid.size() || nexty < 0 || nexty >= grid[0].size()) continue; // 越界了,直接跳过
dfs(grid, visited, nextx, nexty);
}
}
public:
int maxAreaOfIsland(vector<vector<int>>& grid) {
int n = grid.size(), m = grid[0].size();
vector<vector<bool>> visited = vector<vector<bool>>(n, vector<bool>(m, false));
int result = 0;
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
if (!visited[i][j] && grid[i][j] == 1) {
count = 0; // 因为dfs处理当前节点,所以遇到陆地计数为0,进dfs之后在开始从1计数
dfs(grid, visited, i, j); // 将与其链接的陆地都标记上 true
result = max(result, count);
}
}
}
return result;
}
};大家通过注释可以发现,两种写法,版本一,在主函数遇到陆地就计数为1,接下来的相邻陆地都在dfs中计算。 版本二 在主函数遇到陆地 计数为0,也就是不计数,陆地数量都去dfs里做计算。
这也是为什么大家看了很多,dfs的写法,发现写法怎么都不一样呢? 其实这就是根本原因。
以上两种写法的区别,我在题解: DFS,BDF 你没注意的细节都给你列出来了!LeetCode:200. 岛屿数量做了详细介绍。
关于广度优先搜索,如果大家还不了解的话,看这里:广度优先搜索精讲
本题BFS代码如下:
class Solution {
private:
int count;
int dir[4][2] = {0, 1, 1, 0, -1, 0, 0, -1}; // 四个方向
void bfs(vector<vector<int>>& grid, vector<vector<bool>>& visited, int x, int y) {
queue<int> que;
que.push(x);
que.push(y);
visited[x][y] = true; // 加入队列就意味节点是陆地可到达的点
count++;
while(!que.empty()) {
int xx = que.front();que.pop();
int yy = que.front();que.pop();
for (int i = 0 ;i < 4; i++) {
int nextx = xx + dir[i][0];
int nexty = yy + dir[i][1];
if (nextx < 0 || nextx >= grid.size() || nexty < 0 || nexty >= grid[0].size()) continue; // 越界
if (!visited[nextx][nexty] && grid[nextx][nexty] == 1) { // 节点没有被访问过且是陆地
visited[nextx][nexty] = true;
count++;
que.push(nextx);
que.push(nexty);
}
}
}
}
public:
int maxAreaOfIsland(vector<vector<int>>& grid) {
int n = grid.size(), m = grid[0].size();
vector<vector<bool>> visited = vector<vector<bool>>(n, vector<bool>(m, false));
int result = 0;
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
if (!visited[i][j] && grid[i][j] == 1) {
count = 0;
bfs(grid, visited, i, j); // 将与其链接的陆地都标记上 true
result = max(result, count);
}
}
}
return result;
}
};
// DFS
class Solution {
int[][] dir = {
{0, 1}, //right
{1, 0}, //down
{0, -1}, //left
{-1, 0} //up
};
boolean visited[][];
int count;
public int maxAreaOfIsland(int[][] grid) {
int res = 0;
visited = new boolean[grid.length][grid[0].length];
for(int i = 0; i < grid.length; i++){
for(int j = 0; j < grid[0].length; j++){
if(visited[i][j] == false && grid[i][j] == 1){
count = 0;
dfs(grid, i, j);
res = Math.max(res, count);
}
}
}
return res;
}
private void dfs(int[][] grid, int x, int y){
if(visited[x][y] == true || grid[x][y] == 0)
return;
visited[x][y] = true;
count++;
for(int i = 0; i < 4; i++){
int nextX = x + dir[i][0];
int nextY = y + dir[i][1];
if(nextX < 0 || nextY < 0 || nextX >= grid.length || nextY >= grid[0].length)
continue;
dfs(grid, nextX, nextY);
}
}
}
//BFS
class Solution {
int[][] dir = {
{0, 1}, {1, 0}, {0, -1}, {-1, 0}
};
int count;
boolean visited[][];
public int maxAreaOfIsland(int[][] grid) {
int res = 0;
visited = new boolean[grid.length][grid[0].length];
for(int i = 0; i < grid.length; i++){
for(int j = 0; j < grid[0].length; j++){
if(visited[i][j] == false && grid[i][j] == 1){
count = 0;
bfs(grid, i, j);
res = Math.max(res, count);
}
}
}
return res;
}
private void bfs(int[][] grid, int x, int y){
Queue<Integer> que = new LinkedList<>();
que.offer(x);
que.offer(y);
visited[x][y] = true;
count++;
while(!que.isEmpty()){
int currX = que.poll();
int currY = que.poll();
for(int i = 0; i < 4; i++){
int nextX = currX + dir[i][0];
int nextY = currY + dir[i][1];
if(nextX < 0 || nextY < 0 || nextX >= grid.length || nextY >= grid[0].length)
continue;
if(visited[nextX][nextY] == false && grid[nextX][nextY] == 1){
que.offer(nextX);
que.offer(nextY);
visited[nextX][nextY] = true;
count++;
}
}
}
}
}//这里使用深度优先搜索 DFS 来完成本道题目。我们使用 DFS 计算一个岛屿的面积,同时维护计算过的最大的岛屿面积。同时,为了避免对岛屿重复计算,我们在 DFS 的时候对岛屿进行 “淹没” 操作,即将岛屿所占的地方置为 0。
public int maxAreaOfIsland(int[][] grid) {
int res = 0;
for(int i = 0;i < grid.length;i++){
for(int j = 0;j < grid[0].length;j++){
//每遇到一个岛屿就计算这个岛屿的面积同时”淹没“这个岛屿
if(grid[i][j] == 1){
//每次计算一个岛屿的面积都要与res比较,维护最大的岛屿面积作为最后的答案
res = Math.max(res,dfs(grid,i,j));
}
}
}
return res;
}
public int dfs(int[][] grid,int i,int j){
//搜索边界:i,j超过grid的范围或者当前元素为0,即当前所在的地方已经是海洋
if(i < 0 || i >= grid.length || j < 0 || j >= grid[0].length || grid[i][j] == 0) return 0;
//淹没土地,防止后续被重复计算
grid[i][j] = 0;
//递归的思路:要求当前土地(i,j)所在的岛屿的面积,则等于1加上下左右相邻的土地的总面积
return 1 + dfs(grid,i - 1,j) +
dfs(grid,i + 1,j) +
dfs(grid,i,j + 1) +
dfs(grid,i,j - 1);
}class Solution:
def __init__(self):
self.count = 0
def maxAreaOfIsland(self, grid: List[List[int]]) -> int:
# 与200.独立岛屿不同的是:此题grid列表内是int!!!
# BFS
if not grid: return 0
m, n = len(grid), len(grid[0])
visited = [[False for i in range(n)] for j in range(m)]
result = 0
for i in range(m):
for j in range(n):
if not visited[i][j] and grid[i][j] == 1:
# 每一个新岛屿
self.count = 0
self.bfs(grid, visited, i, j)
result = max(result, self.count)
return result
def bfs(self, grid, visited, i, j):
self.count += 1
visited[i][j] = True
queue = collections.deque([(i, j)])
while queue:
x, y = queue.popleft()
for new_x, new_y in [(x + 1, y), (x - 1, y), (x, y - 1), (x, y + 1)]:
if 0 <= new_x < len(grid) and 0 <= new_y < len(grid[0]) and not visited[new_x][new_y] and grid[new_x][new_y] == 1:
visited[new_x][new_y] = True
self.count += 1
queue.append((new_x, new_y))class Solution:
def __init__(self):
self.count = 0
def maxAreaOfIsland(self, grid: List[List[int]]) -> int:
# DFS
if not grid: return 0
m, n = len(grid), len(grid[0])
visited = [[False for _ in range(n)] for _ in range(m)]
result = 0
for i in range(m):
for j in range(n):
if not visited[i][j] and grid[i][j] == 1:
self.count = 0
self.dfs(grid, visited, i, j)
result = max(result, self.count)
return result
def dfs(self, grid, visited, x, y):
if visited[x][y] or grid[x][y] == 0:
return
visited[x][y] = True
self.count += 1
for new_x, new_y in [(x + 1, y), (x - 1, y), (x, y + 1), (x, y - 1)]:
if 0 <= new_x < len(grid) and 0 <= new_y < len(grid[0]):
self.dfs(grid, visited, new_x, new_y)var maxAreaOfIsland = function (grid) {
let dir = [[0, 1], [1, 0], [-1, 0], [0, -1]]; // 四个方向
let visited = new Array(grid.length).fill().map(() => Array(grid[0].length).fill(false))
let dfs = (grid, visited, x, y, m) => {
for (let i = 0; i < 4; i++) {
let nextX = x + dir[i][0]
let nextY = y + dir[i][1]
if (nextX < 0 || nextX >= grid.length || nextY < 0 || nextY >= grid[0].length)
continue;
if (!visited[nextX][nextY] && grid[nextX][nextY] === 1) {
visited[nextX][nextY] = true
m = dfs(grid, visited, nextX, nextY,m+1)
}
}
return m
}
let max = 0
for (let i = 0; i < grid.length; i++) {
for (let j = 0; j < grid[i].length; j++) {
if (!visited[i][j] && grid[i][j] === 1) {
// 深度优先
visited[i][j] = true;
let m = dfs(grid, visited, i, j, 1);
if (m > max) max = m;
}
}
}
return max
};dfs: 版本一
impl Solution {
const DIRECTIONS: [(i32, i32); 4] = [(0, 1), (1, 0), (-1, 0), (0, -1)];
pub fn max_area_of_island(grid: Vec<Vec<i32>>) -> i32 {
let mut visited = vec![vec![false; grid[0].len()]; grid.len()];
let mut res = 0;
for (i, nums) in grid.iter().enumerate() {
for (j, &num) in nums.iter().enumerate() {
if !visited[i][j] && num == 1 {
let mut count = 1;
visited[i][j] = true;
Self::dfs(&grid, &mut visited, (i as i32, j as i32), &mut count);
res = res.max(count);
}
}
}
res
}
pub fn dfs(
grid: &[Vec<i32>],
visited: &mut [Vec<bool>],
(x, y): (i32, i32),
count: &mut i32,
) {
for (dx, dy) in Self::DIRECTIONS {
let (nx, ny) = (x + dx, y + dy);
if nx < 0 || nx >= grid.len() as i32 || ny < 0 || ny >= grid[0].len() as i32 {
continue;
}
let (nx, ny) = (nx as usize, ny as usize);
if !visited[nx][ny] && grid[nx][ny] == 1 {
visited[nx][ny] = true;
*count += 1;
Self::dfs(grid, visited, (nx as i32, ny as i32), count);
}
}
}
}dfs: 版本二
impl Solution {
const DIRECTIONS: [(i32, i32); 4] = [(0, 1), (1, 0), (-1, 0), (0, -1)];
pub fn max_area_of_island(grid: Vec<Vec<i32>>) -> i32 {
let mut visited = vec![vec![false; grid[0].len()]; grid.len()];
let mut res = 0;
for (i, nums) in grid.iter().enumerate() {
for (j, &num) in nums.iter().enumerate() {
if !visited[i][j] && num == 1 {
let mut count = 0;
Self::dfs(&grid, &mut visited, (i as i32, j as i32), &mut count);
res = res.max(count);
}
}
}
res
}
pub fn dfs(
grid: &[Vec<i32>],
visited: &mut [Vec<bool>],
(x, y): (i32, i32),
count: &mut i32,
) {
if visited[x as usize][y as usize] || grid[x as usize][y as usize] == 0 {
return;
}
visited[x as usize][y as usize] = true;
*count += 1;
for (dx, dy) in Self::DIRECTIONS {
let (nx, ny) = (x + dx, y + dy);
if nx < 0 || nx >= grid.len() as i32 || ny < 0 || ny >= grid[0].len() as i32 {
continue;
}
Self::dfs(grid, visited, (nx, ny), count);
}
}
}bfs:
use std::collections::VecDeque;
impl Solution {
const DIRECTIONS: [(i32, i32); 4] = [(0, 1), (1, 0), (-1, 0), (0, -1)];
pub fn max_area_of_island(grid: Vec<Vec<i32>>) -> i32 {
let mut visited = vec![vec![false; grid[0].len()]; grid.len()];
let mut res = 0;
for (i, nums) in grid.iter().enumerate() {
for (j, &num) in nums.iter().enumerate() {
if !visited[i][j] && num == 1 {
let mut count = 0;
Self::bfs(&grid, &mut visited, (i as i32, j as i32), &mut count);
res = res.max(count);
}
}
}
res
}
pub fn bfs(grid: &[Vec<i32>], visited: &mut [Vec<bool>], (x, y): (i32, i32), count: &mut i32) {
let mut queue = VecDeque::new();
queue.push_back((x, y));
visited[x as usize][y as usize] = true;
*count += 1;
while let Some((cur_x, cur_y)) = queue.pop_front() {
for (dx, dy) in Self::DIRECTIONS {
let (nx, ny) = (cur_x + dx, cur_y + dy);
if nx < 0 || nx >= grid.len() as i32 || ny < 0 || ny >= grid[0].len() as i32 {
continue;
}
let (nx, ny) = (nx as usize, ny as usize);
if !visited[nx][ny] && grid[nx][ny] == 1 {
visited[nx][ny] = true;
queue.push_back((nx as i32, ny as i32));
*count += 1;
}
}
}
}
}