Skip to content

Latest commit

 

History

History
177 lines (105 loc) · 6.68 KB

3347.maximum-frequency-of-an-element-after-performing-operations-ii.md

File metadata and controls

177 lines (105 loc) · 6.68 KB
Raw

题目地址(3347. 执行操作后元素的最高频率 II - 力扣（LeetCode）)

https://leetcode.cn/problems/maximum-frequency-of-an-element-after-performing-operations-ii/description/

题目描述

给你一个整数数组 nums 和两个整数 k 和 numOperations 。

你必须对 nums 执行 操作  numOperations 次。每次操作中，你可以：

  • 选择一个下标 i ，它在之前的操作中 没有 被选择过。
  • 将 nums[i] 增加范围 [-k, k] 中的一个整数。

在执行完所有操作以后，请你返回 nums 中出现 频率最高 元素的出现次数。

一个元素 x 的 频率 指的是它在数组中出现的次数。

 

示例 1：

输入：nums = [1,4,5], k = 1, numOperations = 2

输出：2

解释：

通过以下操作得到最高频率 2 ：

  • 将 nums[1] 增加 0 ，nums 变为 [1, 4, 5] 。
  • 将 nums[2] 增加 -1 ，nums 变为 [1, 4, 4] 。

示例 2：

输入：nums = [5,11,20,20], k = 5, numOperations = 1

输出：2

解释：

通过以下操作得到最高频率 2 ：

  • 将 nums[1] 增加 0 。

 

提示：

  • 1 <= nums.length <= 105
  • 1 <= nums[i] <= 109
  • 0 <= k <= 109
  • 0 <= numOperations <= nums.length

前置知识

  • 二分

公司

  • 暂无

思路

容易想到的是枚举最高频率的元素的值 v。v 一定是介于数组的最小值 - k 和最大值 + k 之间的。因此我们可以枚举所有可能得值。但这会超时。可以不枚举这么多么？答案是可以的。

刚开始认为 v 的取值一定是 nums 中的元素值中的一个，因此直接枚举 nums 即可。但实际上是不对的。比如 nums = [88, 53] k = 27 变为 88 或者 53 最高频率都是 1，而变为 88 - 27 = 61 则可以使得最高频率变为 2。

那 v 的取值有多少呢？实际上除了 nums 的元素值，还需要考虑 nums[i] + k, nums[i] - k。为什么呢？

数形结合更容易理解。

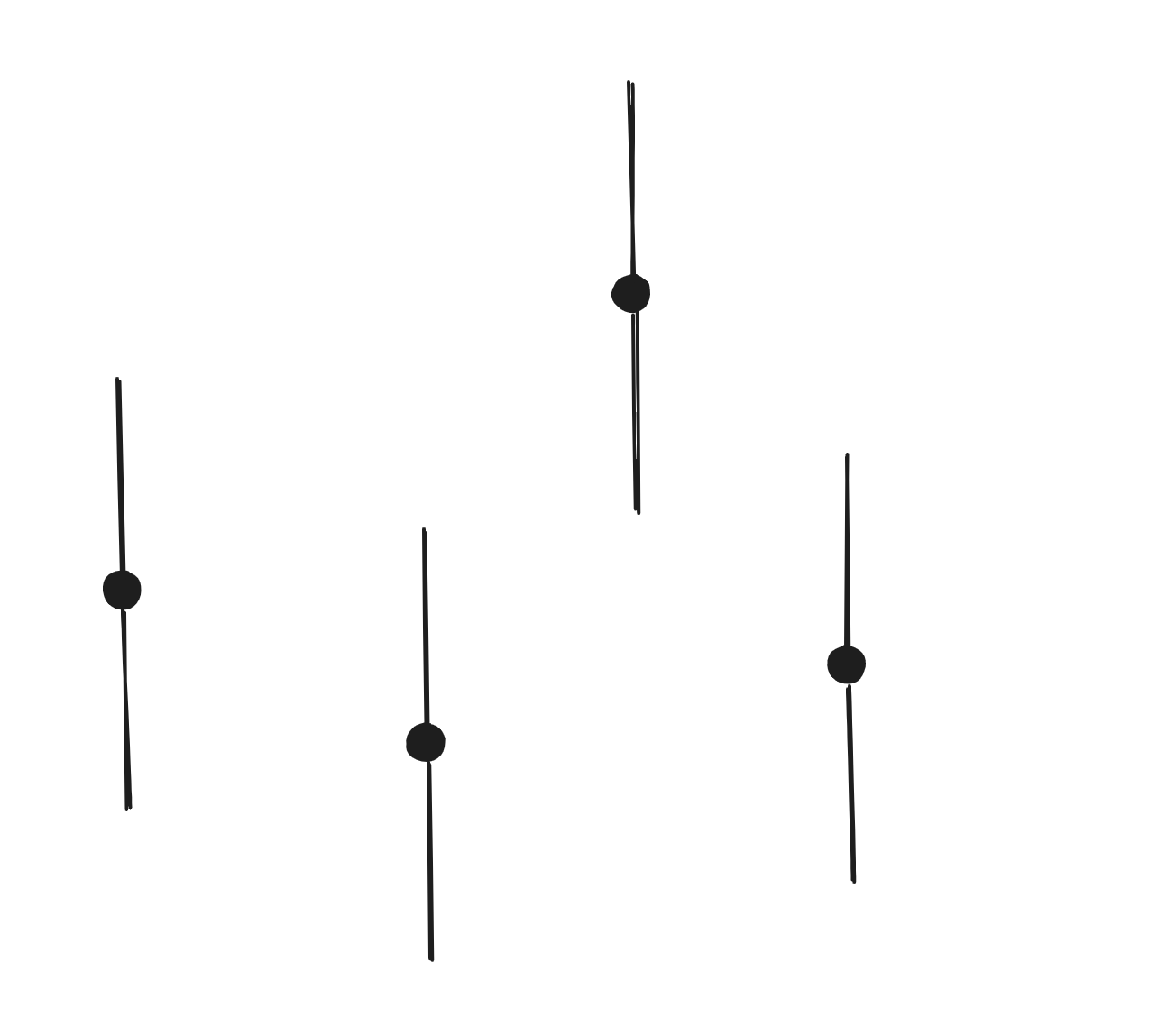
如下图，黑色点表示 nums 中的元素值，它可以变成的值的范围用竖线来表示。

如果两个之间有如图红色部分的重叠区域，那么就可以通过一次操作使得二者相等。当然如果两者本身就相等，就不需要操作。

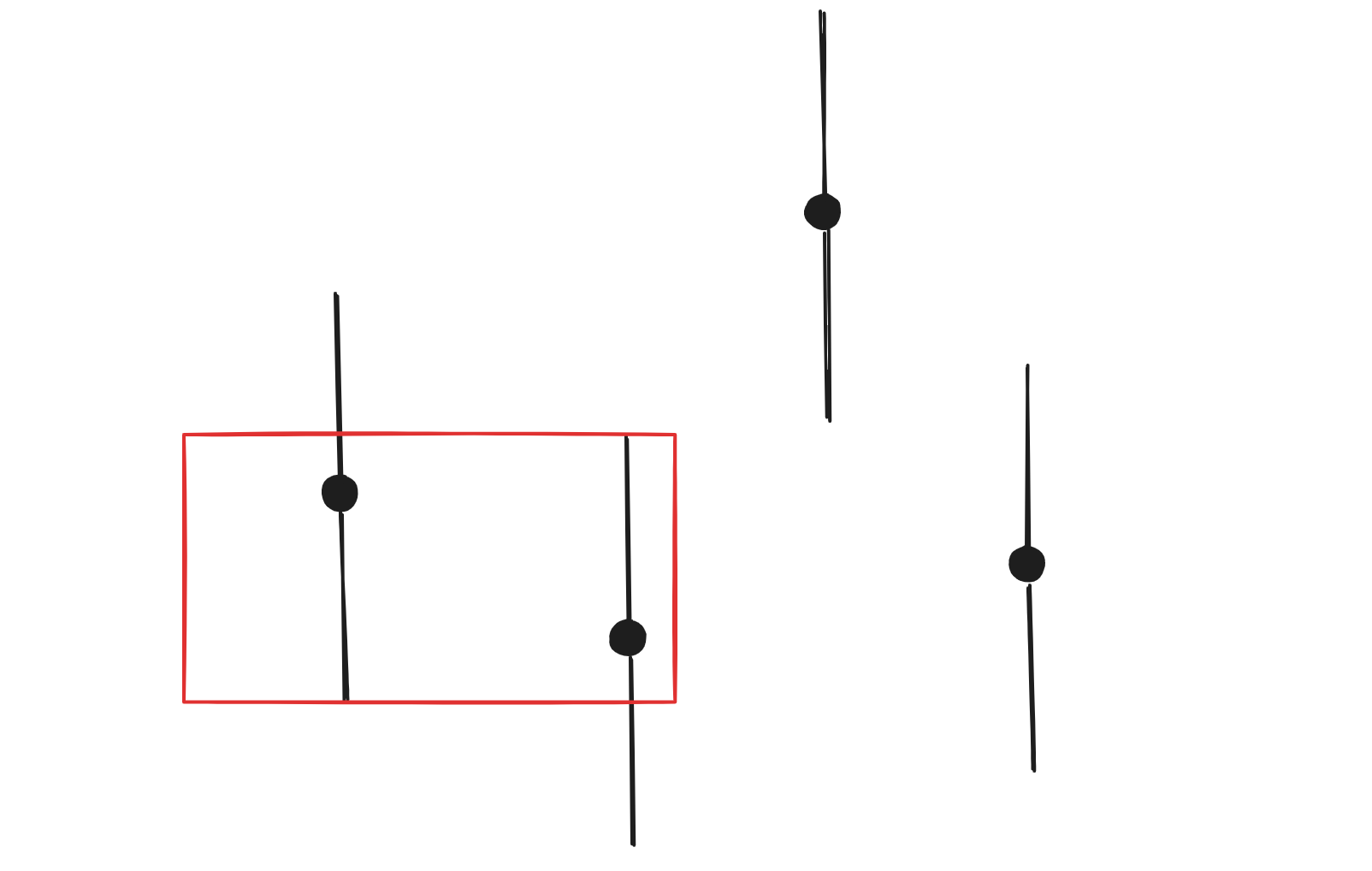
如上图，我们可以将其中一个数变成另外一个数。但是如果两者是下面的关系，那么就不能这么做，而是需要变为红色部分的区域才行。

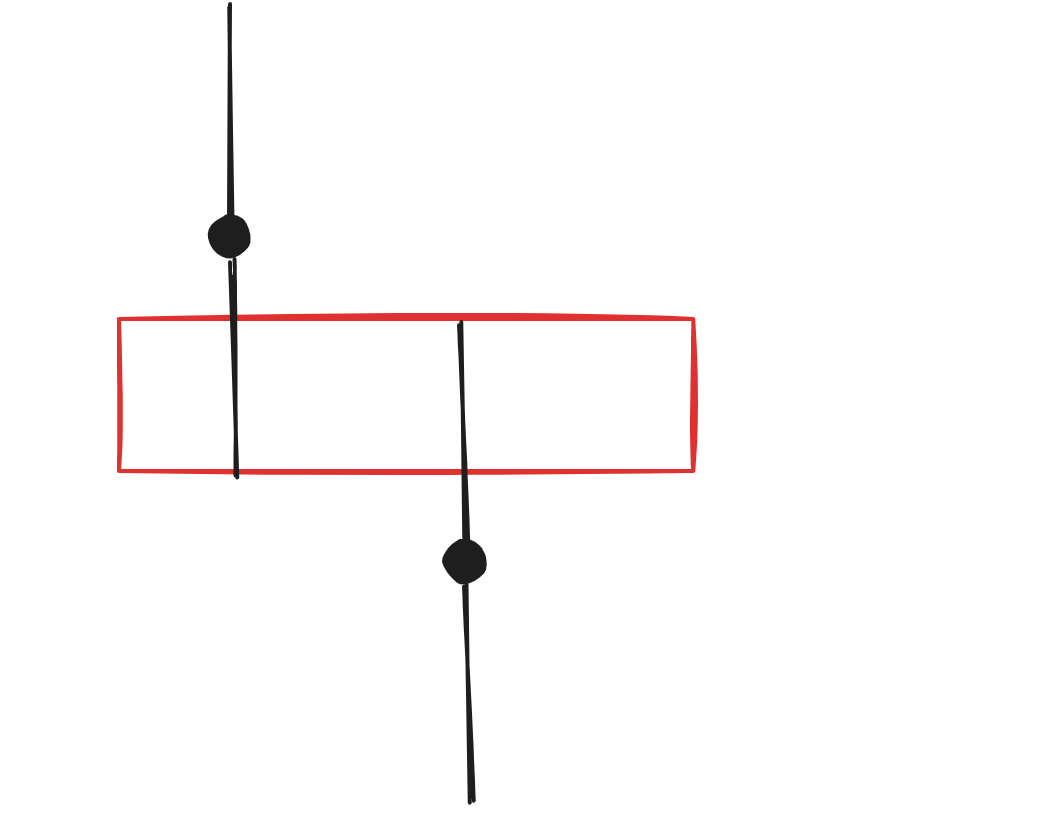
如果更进一步两者没有相交的红色区域，那么就无法通过操作使得二者相等。

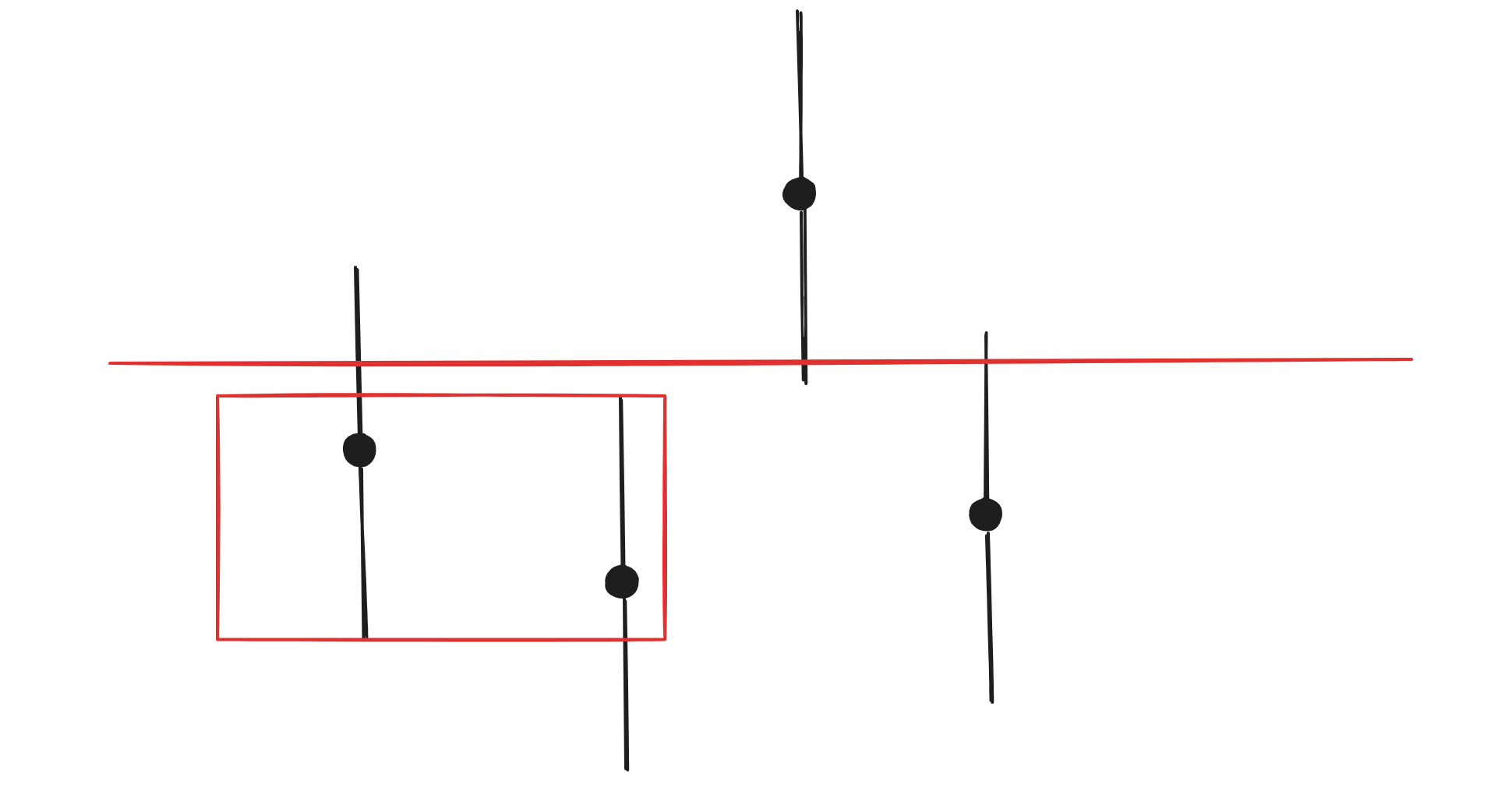
最开始那种朴素的枚举，我们可以把它看成是一个红线不断在上下移动，不妨考虑从低往高移动。

那么我们可以发现红线只有移动到 nums[i], nums[i] + k, nums[i] - k 时，才会突变。这个突变指的是可以通过操作使得频率变成多大的值会发生变化。也就是说，我们只需要考虑 nums[i], nums[i] + k, nums[i] - k 这三个值即可，而不是这之间的所有值。

理解了上面的过程，最后只剩下一个问题。那就是对于每一个 v。找 满足 nums[i] - k <= v <= nums[i] + k 的有几个，我们就能操作几次，频率就能多多少（不考虑 numOperations 影响），当然要注意如果 v == nums[i] 就不需要操作。

具体来说:

  • 如果 nums[i] == v 不需要操作。
  • 如果 nums[i] - k <= v <= nums[i] + k，操作一次
  • 否则，无法操作

找 nums 中范围在某一个区间的个数如何做呢？我们可以使用二分查找。我们可以将 nums 排序，然后使用二分查找找到 nums 中第一个大于等于 v - k 的位置，和第一个大于 v + k 的位置，这两个位置之间的元素个数就是我们要找的。

最后一个小细节需要注意，能通过操作使得频率增加的量不能超过 numOperations。

关键点

  • 枚举 nums 中的元素值 num 和 num + k, num - k 作为最高频率的元素的值 v

代码

  • 语言支持：Python3

Python3 Code:

class Solution:
    def maxFrequency(self, nums: List[int], k: int, numOperations: int) -> int:
        # 把所有要考虑的值放进 set 里
        st = set()
        # 统计 nums 里每种数出现了几次
        mp = Counter(nums)
        for x in nums:
            st.add(x)
            st.add(x - k)
            st.add(x + k)

        # 给 nums 排序，方便接下来二分计数。
        nums.sort()
        ans = 0
        for x in st:
            except_self = (
                bisect.bisect_right(nums, x + k)
                - bisect.bisect_left(nums, x - k)
                - mp[x]
            )
            ans = max(ans, mp[x] + min(except_self, numOperations))
        return ans

复杂度分析

令 n 为数组长度。

  • 时间复杂度：$O(nlogn)$
  • 空间复杂度：$O(n)$

此题解由 力扣刷题插件 自动生成。

力扣的小伙伴可以关注我，这样就会第一时间收到我的动态啦~

以上就是本文的全部内容了。大家对此有何看法，欢迎给我留言，我有时间都会一一查看回答。更多算法套路可以访问我的 LeetCode 题解仓库：https://github.com/azl397985856/leetcode 。 目前已经 54K star 啦。大家也可以关注我的公众号《力扣加加》带你啃下算法这块硬骨头。

关注公众号力扣加加，努力用清晰直白的语言还原解题思路，并且有大量图解，手把手教你识别套路，高效刷题。