-
-
Notifications
You must be signed in to change notification settings - Fork 26
New issue
Have a question about this project? Sign up for a free GitHub account to open an issue and contact its maintainers and the community.
By clicking “Sign up for GitHub”, you agree to our terms of service and privacy statement. We’ll occasionally send you account related emails.
Already on GitHub? Sign in to your account
DDE too stiff? radau method required? #198
Comments
|
I don't have access to a computer right now but two initial observations:
|
|
Excellent suggestions. I'll give it a try when I get a chance and report back. |
|
Sorry for the delay in getting back. I looked at the location of the discontinuity again and you're right, it doesn't correspond to initTauU. I'm not sure why that is the case, I thought they would be the same. I will have to investigate that further. Regardless, I found the discontinuity to occur at I have yet to transform the variables as you suggested. I'm not exactly sure where you would log and where you would exponentiate. Would you log transform the functions (e.g., |
|
At a certain point, you do just need to lower the tolerance to have enough stability on a hard enough problem. |
|
I played around more with the tolerances and dtmax and I now have it working very well. I still find the behaviour a bit strange however. Using Rodas5, I can systematically increase the value of |
|
I think it mostly comes down to hitting the discontinuity right. The closer it accidentally gets to some of the discontinuities, the easier the integration is. That would look pretty random. |
Hi Everyone,
The following is a question I recently asked on Julia Discourse (https://discourse.julialang.org/t/dde-too-stiff-required-tolerances-are-too-slow/52259) about an issue solving a very stiff set of DDEs. I found some improvement by tweaking the solver options (e.g., specifying
dtstops = initTauUanddtmax = 0.1), but Chris thought this might require a radau method so I'm opening this issue in case someone wants to tackle it and use this as a benchmark problem. Any help is greatly appreciated!Original question:
I have a system of DDEs that model host-parasite dynamics in a seasonal environment and I am having some issues because (I think) the equations are so stiff. Basically, when the number of hosts
Sis too high (> about 500) I have to lower the solver tolerances so much that it becomes prohibitively slow (I needSup to about a 4e6). I believe the low tolerances are required becauseu[1]decreases to zero so rapidly whenSis high that the history function (W_past) just returns zero, which makesmatU = 0.0and thereforeu[3]stays at 0.0 (i.e., no infective larvae develop). It may be the case that I just have to use low tolerances and run the simulation for hours and hours, but if anyone has any suggestions to make this work without having to lower the tolerances too much I would be very grateful. I tried several different stiff solvers (Rosenbrock23, Rodas3,4,4P&5, etc.) but without any great success. Maybe some way of adjusting the step size or addressing the discontinuity is possible? Any other general performance tips are also appreciated.Here is a stripped down MWE:
When both the solver tolerances are
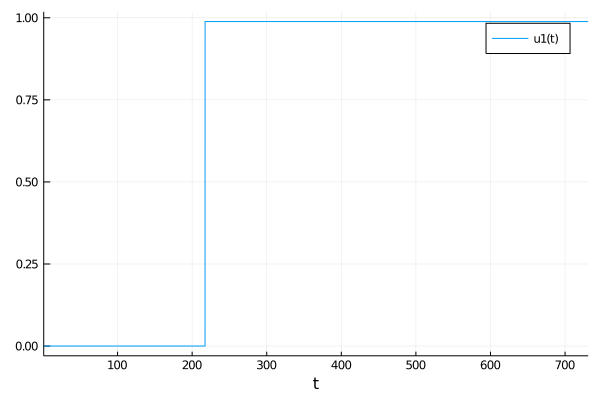
tol = 1e-4andS = 100.0then I get this:But when
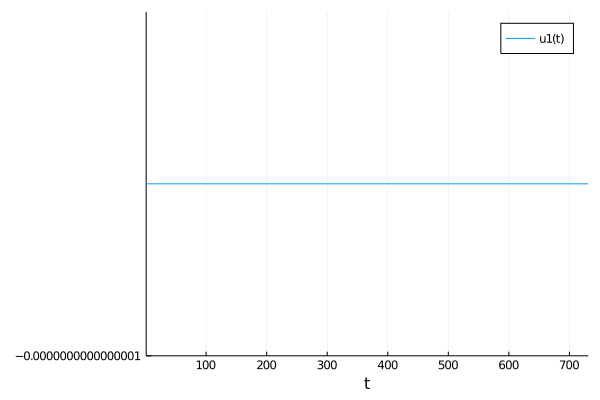
tol = 1e-4andS = 700.0I get this:Once I lower the tolerances to
tol = 1e-6withS = 700.0it works again, but is much much slower and requires larger maxiters. However, with my full model this approach is just too slow, I end up needing to go at least 1e-10 to get anything other than the flat line. I hope I've explained my problem clearly. Thanks.The text was updated successfully, but these errors were encountered: