We read every piece of feedback, and take your input very seriously.
To see all available qualifiers, see our documentation.
Have a question about this project? Sign up for a free GitHub account to open an issue and contact its maintainers and the community.
By clicking “Sign up for GitHub”, you agree to our terms of service and privacy statement. We’ll occasionally send you account related emails.
Already on GitHub? Sign in to your account
In particular https://github.com/sintefmath/Splipy/blob/f7bf4ef8e2a15433ec9ac16498b2275cc44e265f/splipy/utils/refinement.py#L14 should accept as input argument obj a SplineModel. This should take advantage of neighbourhood information to propagate refinement across the domain.
obj
SplineModel
In particular, the following script:
from splipy import * from splipy.io import G2 from splipy.utils import refinement import splipy.curve_factory as cf import splipy.surface_factory as sf import numpy as np from numpy import sin, cos, arctan2, pi, sqrt, tan # units in mm R = 3 # radius α = pi/6 # inlet angle l1 = 20 # counterflow length (left side) l2 = 10 # directedflow length (right side) l3 = 10 # length before circular arc w = 4 # channel width # first patch patches = [Surface()*[l3, w]] patches[-1][0,-1] = [-w/2/sin(α),w] # compute the circle-channel intersection point(s) b = -2*R*sin(α)-2*l3*cos(α) c = l3**2 t1 = (-b+sqrt(b**2-4*c))/2 x1 = t1*cos(α) y1 = -t1*sin(α) crv1 = cf.circle_segment_from_three_points([l3,0], [l3+R,-R], [x1,y1]) b = -2*R*sin(α)-2*l3*cos(α) c = l3**2 - 2*R*w - w**2 t2 = (-b+sqrt(b**2-4*c))/2 x2 = t2*cos(α) y2 = -t2*sin(α) crv2 = cf.circle_segment_from_three_points([l3,w], [l3+R+w,-R], [x2,y2]) # crv0 = cf.circle(center=[l3,-R], r=R) # debug help curve patches.append(sf.edge_curves(crv1,crv2)) crv3 = cf.line([ 0,0], t1* np.array([cos(α), -sin(α)])) crv4 = cf.line([-w/sin(α),0],(t1+w*cos(α))*np.array([cos(α), -sin(α)]), relative=True) patches.append(sf.edge_curves(crv3,crv4)) crv3 = cf.line([x1,y1], (t2-t1)*np.array([cos(α), -sin(α)]), relative=True) crv4 = cf.line(patches[-1][-1], patches[1][-1][:2] + w*np.array([-sin(α), -cos(α)])) patches.append(sf.edge_curves(crv3,crv4)) crv3 = cf.line([ 0,0], [-w/2/sin(α),w]) crv4 = cf.line([-w/sin(α),0], -w/sin(α)*np.array([cos(α), -sin(α)]), relative=True) patches.append(sf.edge_curves(crv3,crv4)) crv3 = patches[-1].edges()[-1] crv4 = cf.line([-l1,0], [-l1,w]) patches.append(sf.edge_curves(crv3,crv4)) crv3 = patches[3].edges()[1] crv4 = crv3 + l2*np.array([cos(α), -sin(α)]) patches.append(sf.edge_curves(crv3,crv4)) # make all patches compatible for p in patches: p.force_rational() dp = np.array([3,3]) - p.order() p.set_order(3,3) with G2("multipatch.g2") as f: f.write(patches)
Which is producing the following 6-patch geometry
Should after calling
refinement.edge_refine(patches[0], S=3, direction='v', n=15) refinement.edge_refine(patches[-1], S=3, direction='u', n=15)
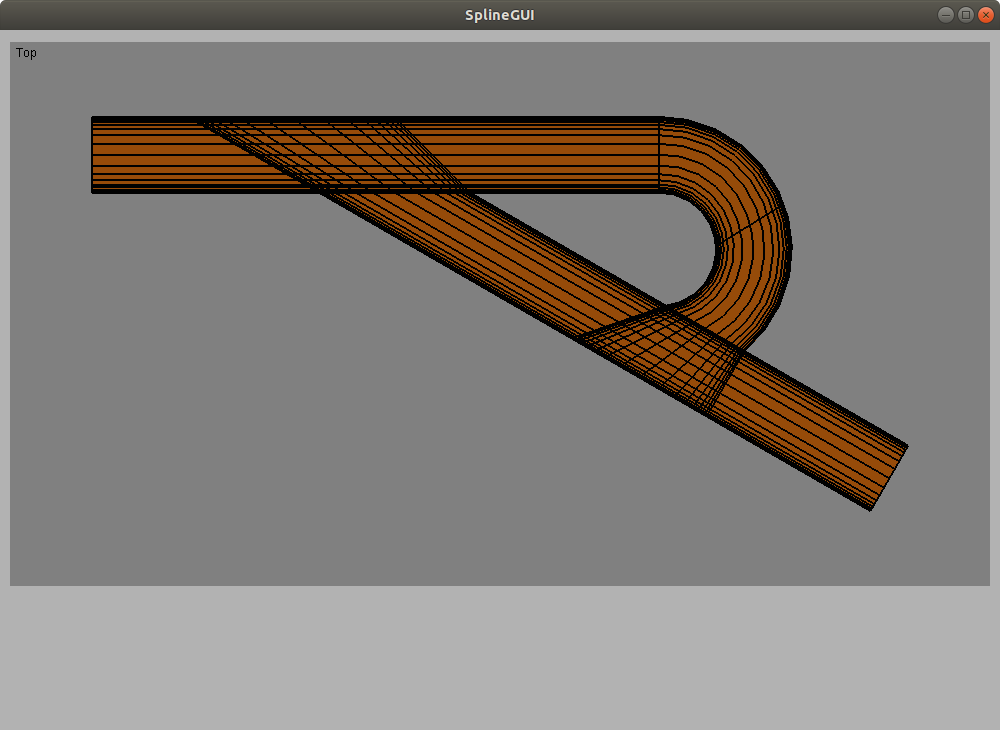
Produce the following refinement
The text was updated successfully, but these errors were encountered:
Similar changes should also be made to
https://github.com/sintefmath/Splipy/blob/f7bf4ef8e2a15433ec9ac16498b2275cc44e265f/splipy/utils/refinement.py#L67
Sorry, something went wrong.
No branches or pull requests
In particular https://github.com/sintefmath/Splipy/blob/f7bf4ef8e2a15433ec9ac16498b2275cc44e265f/splipy/utils/refinement.py#L14 should accept as input argument
objaSplineModel. This should take advantage of neighbourhood information to propagate refinement across the domain.In particular, the following script:
Which is producing the following 6-patch geometry
Should after calling
Produce the following refinement
The text was updated successfully, but these errors were encountered: