README.rst

NTracer

A hyper-spacial ray-tracing library

NTracer is a simple ray-tracer that can work with scenes with an arbitrary number of dimensions.

A three-dimension slice of a six-dimensional hypercube

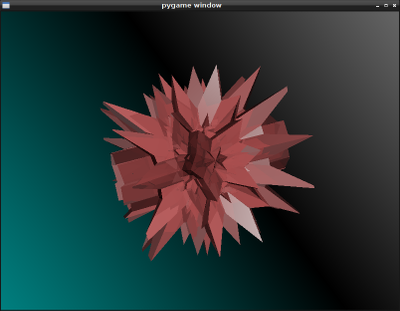
A three-dimension slice of a great grand stellated 120-cell

The renderer can use an arbitrary number of threads and by default uses as many threads as there are CPU cores. For small dimensionalities (by default, eight or fewer dimensions), the library uses specialized routines with the number of dimensions hard-coded, which offer better performance by avoiding the looping and heap allocation that the generic versions require.

The main goal is to aid in the visualization of higher-dimensional space. Note that this ray-tracer has a very limited feature-set and is not as efficient as it could be for 3D.

There is special support for Pygame, but it is not a requirement. However, the included example scripts, hypercube.py and polytope.py, depend on it.

Documentation is available at https://rouslan.github.io/NTracer/doc.

Building and Installing from Source

Building from source requires a compiler with C++17 plus designated initializer support.

If building on a machine with multiple CPU cores, it is recommended you use the -j flag with the number of available cores, up to 7 (there are 7 extension modules to compile), e.g.: "python setup.py build -j 7 install". This will reduce the amount of time needed to compile.

Unix-like systems

To install from source, type "python setup.py install" in the source's directory (where setup.py is located).

Alternatively a package manager such as pip can be used (pip install ntracer) to download, build and install this package in one step.

Windows

To compile with the default windows compiler (Microsoft Visual C++), you need at least the 2019 version. However, the 2019 version (the latest version at the time of this writing) produces a significantly slower binary. To compile with MSVC anyway, follow the steps described in "Unix-like systems" above.

The recommended way to compile is with MinGW-w64 (MinGW32 lacks the needed C++ thread library). Despite the name, it doesn't require a 64-bit version of Windows. It doesn't matter how Python itself was compiled.

To build with MinGW-w64, execute the following commands in the package source directory (where setup.py is located):

set PATH=<base path of MinGW-w64>\bin;%PATH%
<Python install directory>\python.exe setup.py build --compiler=mingw32 install

By default, the build command will also copy any MinGW-w64 DLLs that the binaries require into the installation directory (technically it only copies the DLLs into the temporary build directory and the install command does the installing). To suppress this behaviour (which you may want to do if the MinGW-w64 bin directory is already in the system-wide path), use the build flag --copy-mingw-deps=false.

Customization

When compiling under GCC or Clang, the setup script will use the -march=native parameter to use the most recent instruction set that the current CPU supports. To override this or for any other customization, the build command supports the flag --cpp-opts=<options> which will add the specified options to the end of the argument list when invoking the compiler. There is also the flag --ld-opts=<options> for adding linker options. To remove arguments that lack a negative form, you can use --cpp-neg-opts=<options> and --ld-neg-opts=<options>, where options is a space-separated list of strings that will be removed from the list of compiler and linker options respectively.

MSVC lacks an equivalent to -march=native and also has less fined-grained control over SSE/AVX options. Thus, when building with MSVC, a small program is first built, that checks the capabilities of the current CPU. This can be suppressed by adding --test-cpu-flags=false to the build command.

For controlling the SSE/AVX instructions used, the compiler's /arch flag can be used (e.g. --cpp-opts=/arch:AVX512), but for finer grained control, any of the following macros may be also defined:

• SUPPORT_SSE
• SUPPORT_SSE2
• SUPPORT_SSE3
• SUPPORT_SSSE3
• SUPPORT_SSE4_1
• SUPPORT_SSE4_2
• SUPPORT_AVX
• SUPPORT_AVX2
• SUPPORT_AVX512F

where each one of these implies all of macros above it.

The following can also be defined:

• SUPPORT_AVX512BW
• SUPPORT_AVX512CD
• SUPPORT_AVX512DQ
• SUPPORT_AVX512ER
• SUPPORT_AVX512PF
• SUPPORT_AVX512VL

which are independent of each other. Note that not all of these instruction sets will necessarily be used, but they are still available for future compatibility.

Even when using these macros, the /arch flag should still be used for maximum benefit. E.g. for 32-bit systems: --cpp-opts="/arch:SSE2 /DSUPPORT_SSE4_1" (the /arch:SSE2 option is not present for 64-bit systems because x86-64 always supports SSE2).

These macros can also be defined for GCC/Clang, but those compilers have flags for each of these instruction sets already.

Building Documentation

Note that you must first build the package and it must be made importable (either by installing it or by setting the PYTHONPATH environment variable to where it was built), because some of the documentation is pulled from the doc-strings.

To generate the documentation, run python setup.py build_sphinx. Sphinx, LaTex and dvipng are required.

Dealing with Higher-Dimensional Space

Regardless of the number of dimensions of the scene, the images produced by the ray-tracer are always taken from the view-point of a three-dimensional observer. A two-dimensional image is produced by projecting rays from a single point, onto a grid corresponding to the pixels of the image. The consequence of this is that the observer can only see a three-dimensional slice of the entire scene with a single image. The reason for this can be understood by imagining a lower-dimensional analog. If a being existed in a two-dimensional universe, it would only be able to see in two dimensions and have three degrees of freedom (two translation and one rotation components). If the being were plucked from its universe and placed before a three-dimensional object, it would only be able to see a two-dimensional slice of the object at any given time. To see the rest of the object, the being would have to either translate or rotate itself in a way that exploits one of the newly acquired degrees of freedom (one new translation and two new rotation components).

Having more than three dimensions, it no longer makes sense to rotate about a single axis. Thus the static member function Matrix.rotation, which creates a rotation matrix, requires two vectors to describe a plane of rotation.

Normally, cross products can only be computed in three-dimensional space. To find perpendicular vectors, the function cross provides a generalized version, which takes a sequence of D-1 linearly independent vectors, where D is the dimensionality of the scene.

In three-dimensional space, the surface of a solid object can be constructed out of triangles. However, it is impossible to fully enclose objects with more than three dimensions using a finite number of triangles, just as three-dimensional objects cannot be enclosed using a finite set of lines or points. Therefore, instead of triangles, n-dimensional simplexes, where n is one less than the number of dimensions of the scene, are used instead. One may be tempted to point out that a 3-simplex (three-dimensional simplex, i.e. a tetrahedron) can be built out of triangles, a 4-simplex can be built out of 3-simplexes and so on, so one should still be able to use triangles to build higher dimensional objects, but this is not quite correct. Technically, you can only construct the hull of a 3-simplex. In four-dimensional space, a line can pass through a 3-simplex without intersecting any of its faces. In fact, orienting a line so it does intersect a face would be like trying to stab a line of zero thickness with a needle of zero thickness in three-dimensional space. It only gets worse with even more dimensions. The simplex class provided by this library (which is actually named Triangle) is continuous between every point and avoids this problem.