Bài toán tám quân hậu là bài toán đặt tám quân hậu trên bàn cờ vua kích thược 8×8 sao cho không có quân hậu nào có thể ăn được quân hậu khác. Do đó lời giải cho bài toán là sắp xếp tám quân hậu trên bàn cờ sao cho không có hai quân hậu nào cùng hàng, cùng cột hoặc cùng đường chéo. Bài toán tám quân hậu là ví dụ cho câu đố n quân hậu trên bàn cơ kích thước n×n, lời giải chỉ tồn tại khi n là một số tự nhiên và lớn hơn hoặc bằng 4.
Ví du, lời giải cho bài toán 4 quân hậu.
Đầu ra sẽ là một ma trận nhị phân với 1 là vị trí đặt quân hậu, ví dụ dưới đây là ma trận kết quả cho bài toán 4 quân hậu.
{ 0, 1, 0, 0}
{ 0, 0, 0, 1}
{ 1, 0, 0, 0}
{ 0, 0, 1, 0}
Tạo tất cả các hình trạng có thể có của các quân hậu trên bàn cờ và in ra một hình trạng thoã mãn các ràng buộc đã cho.
while there are untried configurations
{
generate the next configuration
if queens don't attack in this configuration then
{
print this configuration;
}
}
Ý tưởng là đặt mỗi quân hậu trên các cột khác nhau, từ cột bên trái ngoài cùng. Khi đặt quân hậu vào một cột, ta kiểm tra xem có đụng độ với các quân hậu đã đặt trước đó hay không. Tại cột hiện tại, nếu ta thấy một hàng không có đụng độ, ta đánh dấu hàng đó và cột đó là một phần của lời giải. Nếu ta không tìm thấy được hàng nào ta quay lùi về và báo false.
1) Bắt đầu từ cột bên trái
2) Nếu tất cả hậu đều đã đặt xong trả về true
3) Thử tất cả hàng với cột hiện tại.
a) Nếu quân hậu có thể đặt vào hàng thì đánh dấu [row, column] là một phần của lời giải và đệ quy kiểm tra xem quân hậu ở đây có thể dẫn đến lời giải pháp không.
b) Nếu đặt quân hậu tại [row, column] dẫn đến lời giải thì trả về true.
c) Nếu đặt quân hậu không dẫn đến lời giải thì bỏ đánh dấu [row, column] (Quay lùi) và thử tiếp ở hàng khác.
3) Nếu đã thử tất cả hàng vẫn không hoạt động, trả về false để kích hoạt quay lùi
Giải thuật bit giải quyết vấn đề như sau:
-
Quân hậu có thể ăn theo đường chéo, ngang hoặc dọc. Do dó chỉ có thể có một quân hậu trong mỗi hàng, mỗi cột và mỗi đường chéo.
-
Vì ta biết chỉ có một quân hậu mỗi hàng, ta sẽ bắt đầu ở hàng đầu tiên, đặt quân hậu ở hàng thứ hai, ... cho đến khi a) ta có được lời giải hợp lệ b) ta đi vào ngõ cụt (tức là ta không thể đặt quan hậu sao cho nó an toàn với các quân hậu khác)
-
Vì ta chỉ đặt một quân hậu vào mỗi hàng nên ta không cần lo lắng việc bị ăn theo chiều ngang. Điều đó có nghĩa ta chỉ cần kiểm tra 3 thứ khi đặt quân hậu
- Cột không có quân hậu nào khác
- Đường chéo trái không có quân hậu nào khác
- Đường chéo phải không có quân hậu nào khác
-
Nếu ta đặt ở một điểm mà không có vị trí nào an toàn để đặt quân hậu, ta phải từ bỏ vị trí hiện tại và triển khai một ví trí khác.
Nói về hàm đệ quy, ta lưu ý 3 tham số là lefftDiagonal, 'columnvàrightDiagonal. Mỗi tham số đều là số nguyên, nhưng điểm mảng của giải thuật này là số nguyên có thể biểu diễn bằng một chuỗi tuần tự bit. Thế nên, ta có thể hiểu mỗi tham số là một chuỗi tuần tự N` bit.
Mỗi bit của mỗi tham số sẽ biểu diễn vị trí đã có quân hậu với hàng hiện tại.
Ví dụ
- Cho
N=4, cột có giá trị0010nghĩa là cột thứ 3 đã có quân hậu - Cho
N=8, đường chéo trái có giá trị00011000trên hàng thứ 5 có nghĩa là đường chéo trái đi xuyên qua cột thứ 4 và 5 với hàng đã có quân hậu
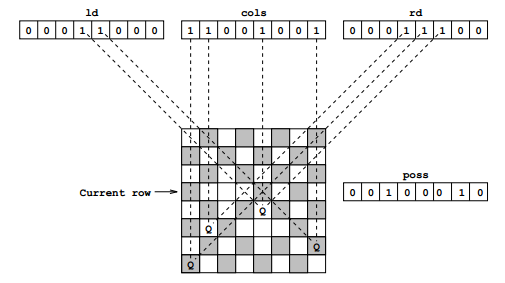
Ảnh minh hoạ bên dưới cho leftDiagonal, column, và rightDiagonal