Author: Philip Franz
Kratos version: 9.5
Source files: cylinder_on_inclined_plane_2D
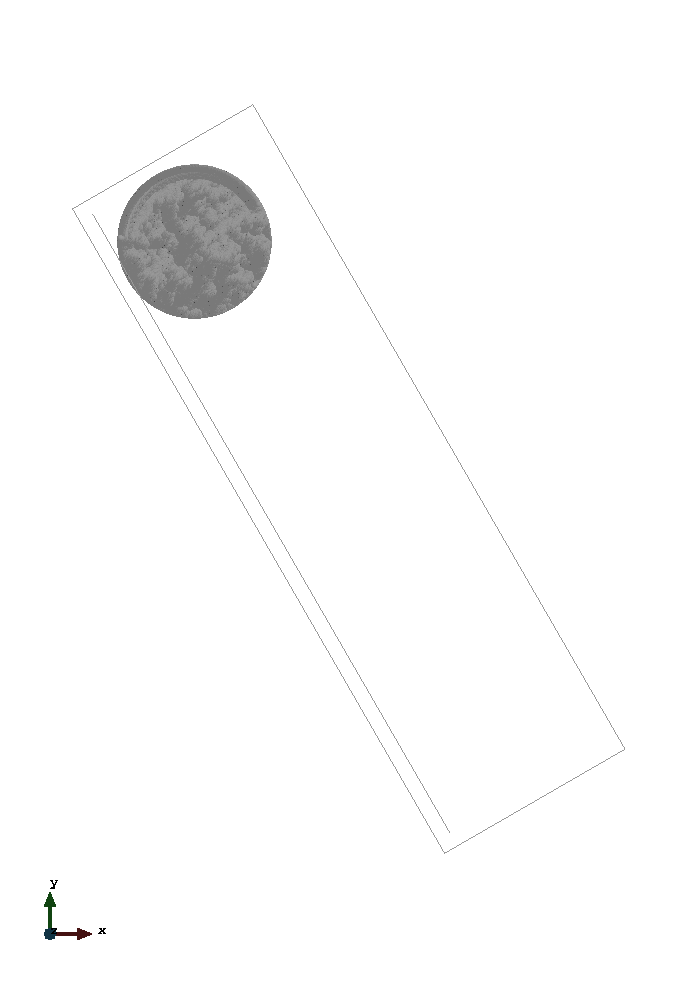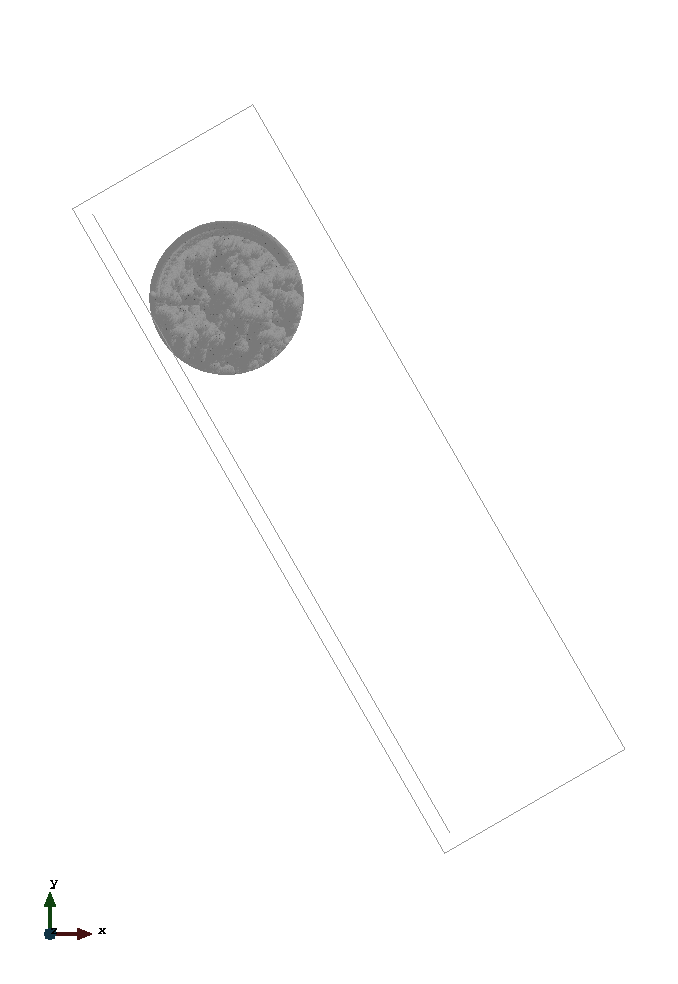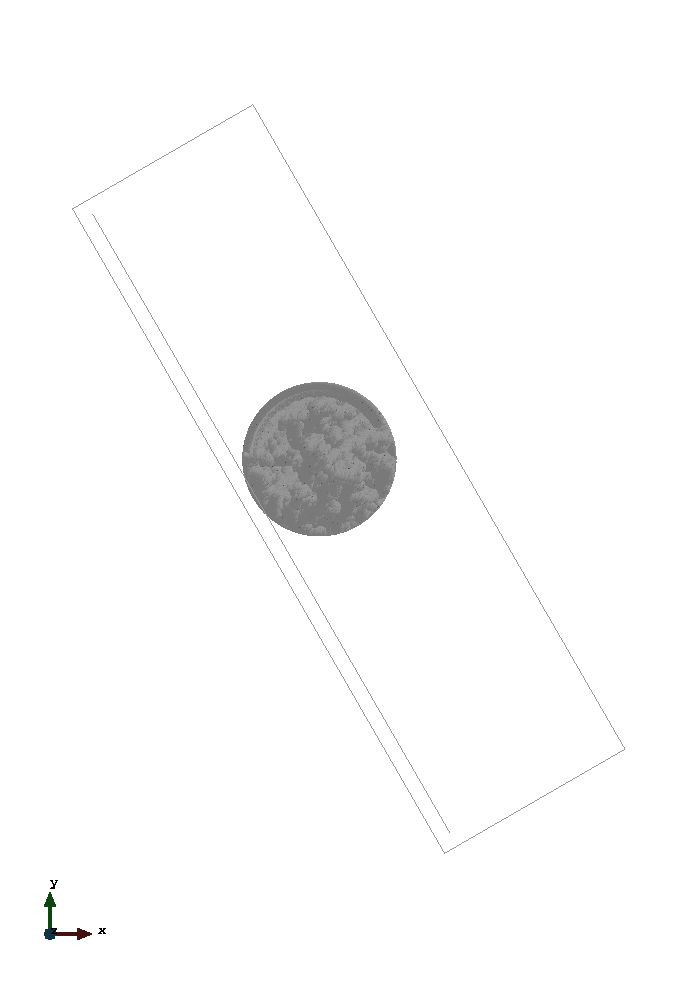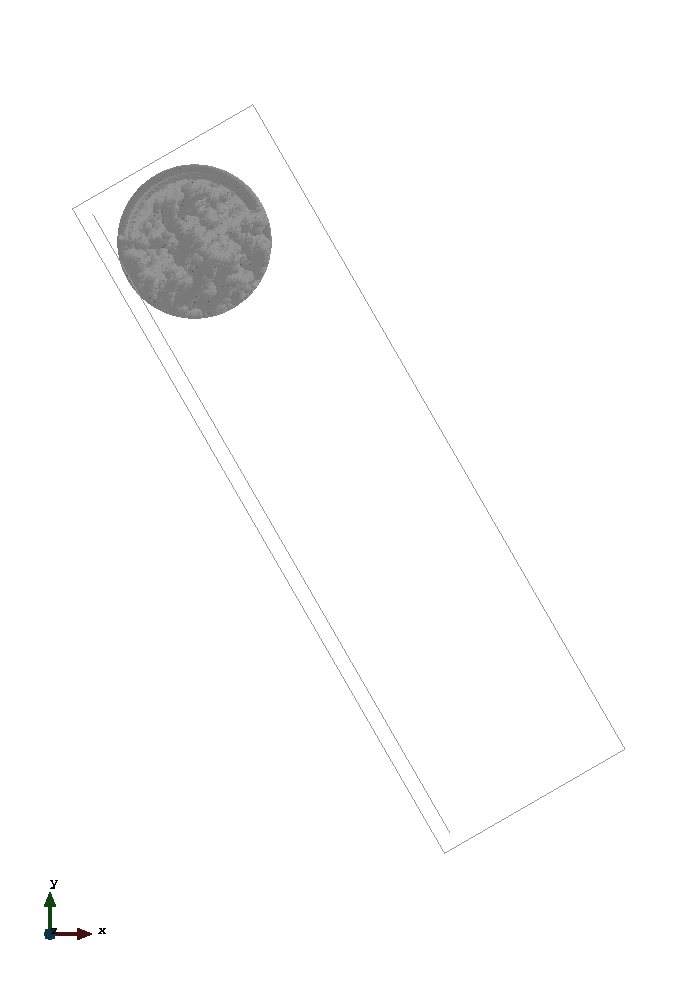
This is a 2D simulation of a cylinder on an inclined plane. A rotating as well as a frictionless sliding behaviour of the cylinder are regarded subsequently. The simulation is set up according to section 4.5.2 of (Iaconeta, 2019). Linear, unstructured, triangular elements with a size of 0.01m are used to initialize the MPs. Three MPs per cell are considered. For the backgroundmesh linear, unstructured, triangular elements with a size of 0.02m are used. However, in contrast to section 4.5.2 of (Iaconeta, 2019), the inclined plane is modelled by a line with unstructured elements with size 0.01m. On that line a non conforming Dirichlet boundary condition is imposed by using the penalty method based on (Chandra et al., 2021).
The following applications of Kratos are used:
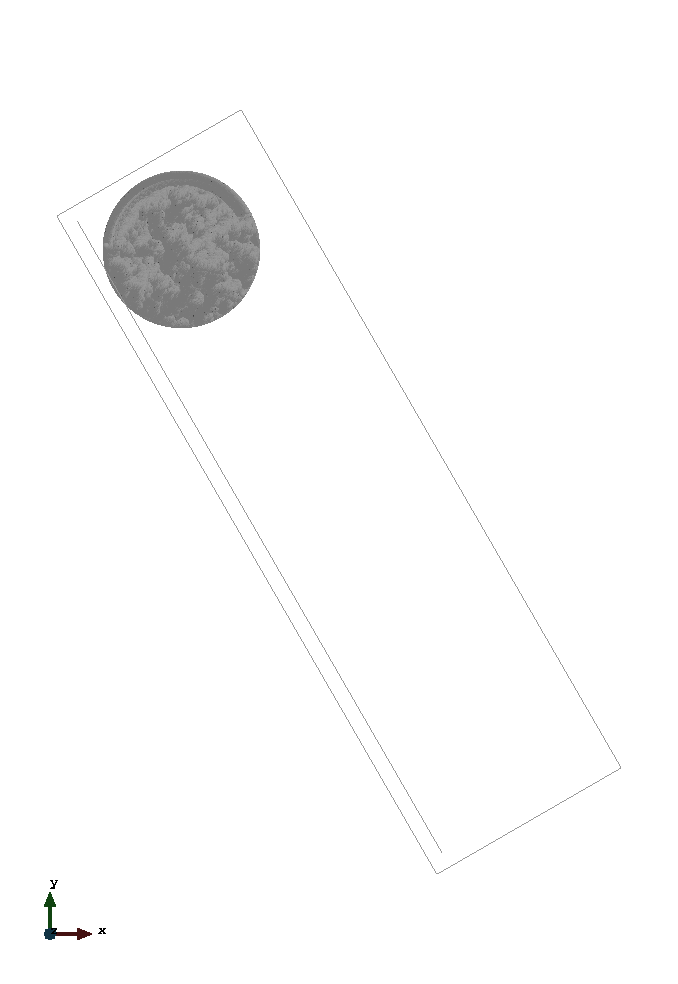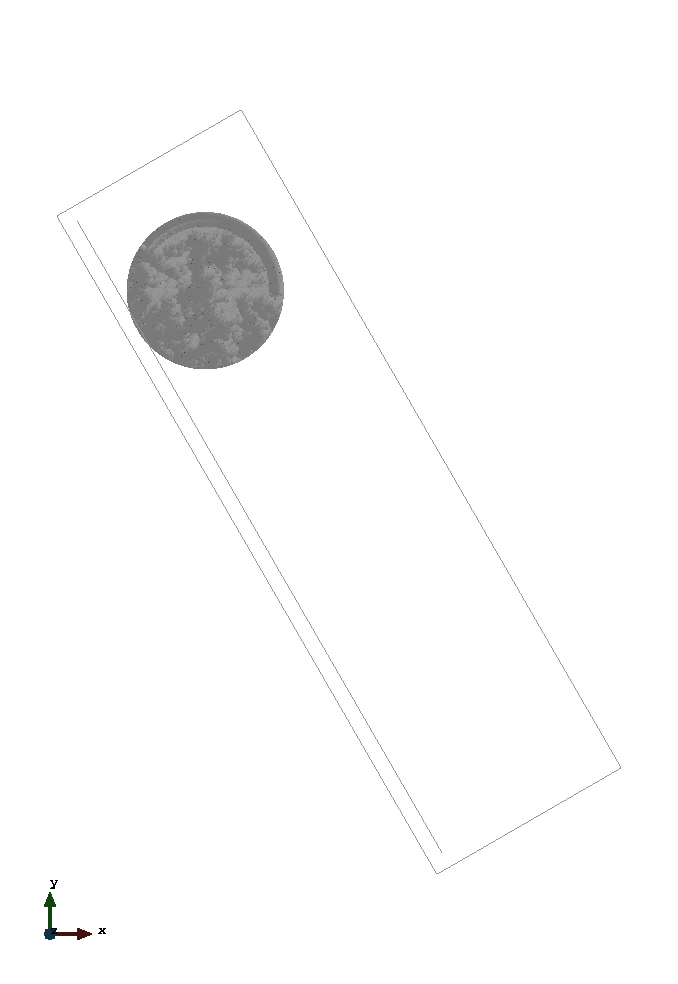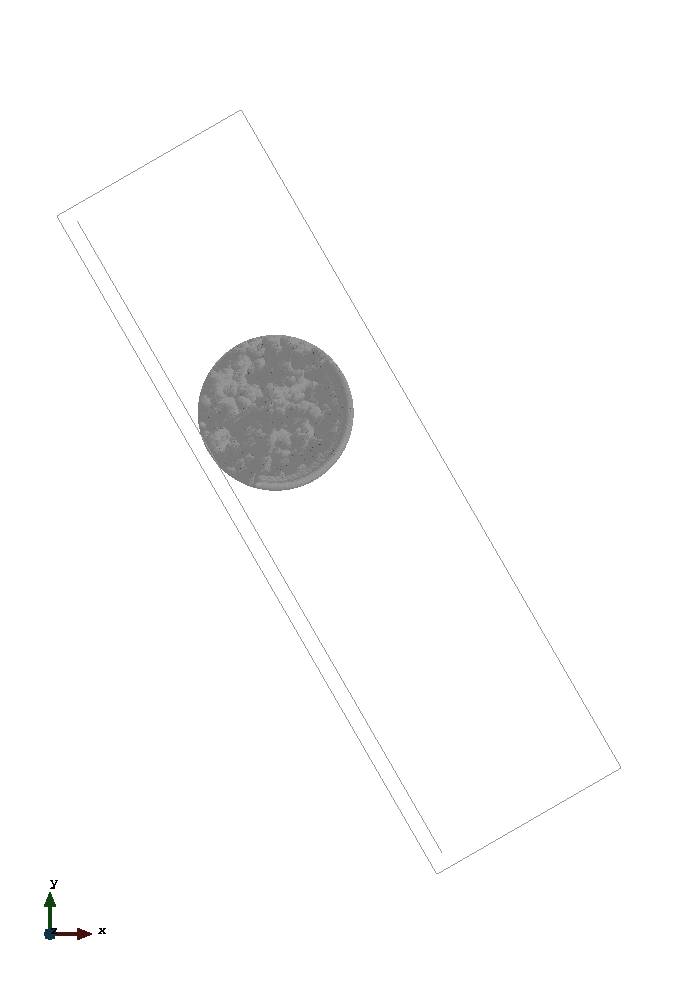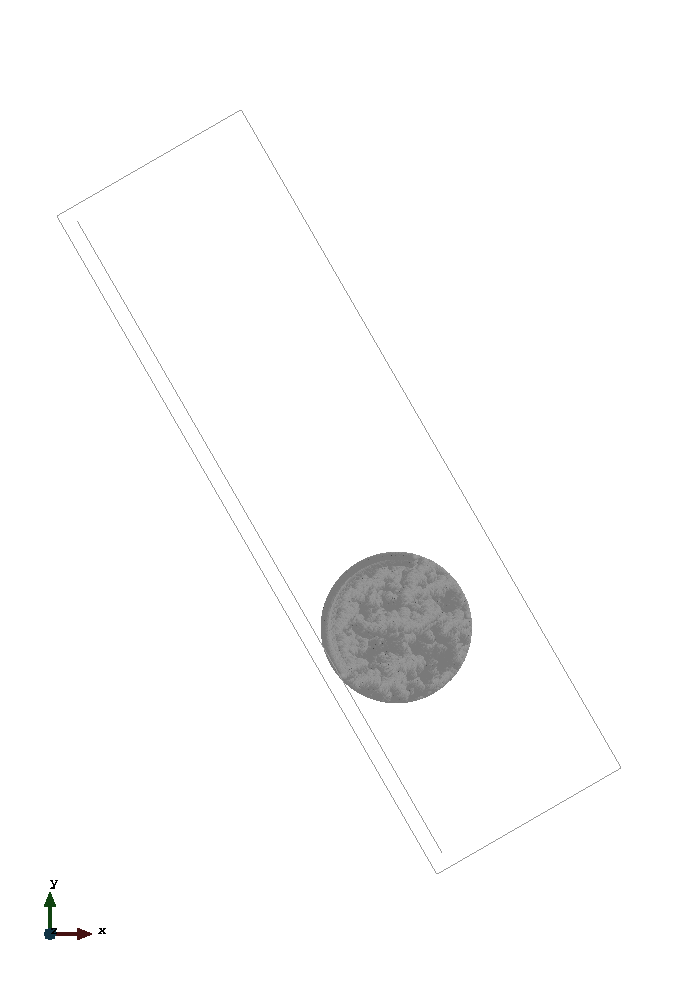
The problem geometry as well as the boundary conditions are sketched below. The non conforming boundary condition is respresented by the copper coloured line.
A hyper elastic Neo Hookean Plane strain (2D) constitutive law with unit thickness is considered with the following material parameters:
- Density (ρ): 7800 Kg/m3
- Young's modulus (E): 200 MPa
- Poisson ratio (ν): 0.3
The time step is 0.001 seconds; the total simulation time is 1.0 seconds. The angle (α) of the inclined plane is 60°. The penalty-factor is 1e13.
The contact between cylinder and inclined plane is modelled with the option "contact" (see line 53, file ProjectParameters_contact.json) in the first and with "slip" in the second case, based on (Chandra et al., 2021). Choosing "contact" leads to a rolling behaviour of the cylinder; "slip" to frictionless sliding.
The analytical and numerical solution for the displacement function of the respective case of the above stated problem are compared afterwards:
The left image displays the rolling cylinder - modelled with option "contact". The right one shows the sliding cylinder (frictionless) - modelled with option "slip".
- Iaconeta, I. (2019). Discrete-continuum hybrid modelling of flowing and static regimes, Ph.D. thesis, Universitat Politècnica de Catalunya, Barcelona
- Chandra, B., Singer, V., Teschemacher, T., Wuechner, R., & Larese, A. (2021). Nonconforming Dirichlet boundary conditions in implicit material point method by means of penalty augmentation, Acta Geotechnica, 16(8), 2315-2335. DOI: 10.1007/s11440-020-01123-3.