-
Notifications
You must be signed in to change notification settings - Fork 48
New issue
Have a question about this project? Sign up for a free GitHub account to open an issue and contact its maintainers and the community.
By clicking “Sign up for GitHub”, you agree to our terms of service and privacy statement. We’ll occasionally send you account related emails.
Already on GitHub? Sign in to your account
How does xESMF treat missing values? #22
Comments
|
It seems that The ESMF docs show a usage that looks something like: regrid = ESMF.Regrid(srcfield, dstfield,
regrid_method=ESMF.RegridMethod.NEAREST_DTOS,
unmapped_action=ESMF.UnmappedAction.ERROR,
src_mask_values=mask_values) |
|
In ESMPy, the mask is configured on the grid and "selected" in the regrid call. You'll need to merge any data variable masks with any spatial masks and set that on the grid (see this code for an example). You can then select the value used by ESMF to construct the mask in the regrid call. The When masking, also pay attention to the |
|
Xarray uses |
|
@jhamman The different behaviors you get from bilinear and conservative algorithms are actually expected. The handling of
When coarse-graining, conservative regridding will average over a large number of small cells (8*8=64 in your case), while bilinear regridding will only average over the nearest 4 cells. That's why you see a lot of I am not sure if an additional option for masking is needed. If I understand correctly, ESMPy's masking capability can be equivalently done by masking the input/output data itself, before or after the regridding computation. |
|
@JiaweiZhuang and @bekozi - thank you both for sticking with this issue. I am starting to understand the situation a bit better.
As a bottom line, I think it is incorrect to let xarray's mask nans propagate through regridding operations. Most of xarray's operators are nan skipping so it seems logical to me, that xESMF would take a similar approach. I also want to be clear, I'm not asking anyone to do any work here. I'm mostly trying to understand the challenges in this area. If we can settle on a path forward, I wouldn't be surprised if I would contribute to this development. |
It is true that Or do you mean some sort of "re-normalizing"? Say, if the weights for a destination point are |
Something like that. I image that is how ESMpy uses the masks internally. Perhaps @bekozi can elaborate thought. |
|
There's quite a bit going on this discussion, so I apologize for glossing over anything... @JiaweiZhuang is correct regarding the way masks are handled for the conservative case. Masks will drop cells if only one masked cell is mapped to a destination cell. I don't have any experience working with If configured properly, the mask on the source grid will lead to an appropriate normalization for weight factors with masked entries excluded in the final weight matrix. The destination mask will simply exclude entries in the weight matrix for its associated index. Dynamic masking (changing mask with time/level) was implemented recently in ESMF, but I think that is beyond the scope of this discussion. Without fully understanding
This will generally work, but may lead to different masked data and values when compared with a regrid + mask.
Nothing like this that I'm aware of! |
Thanks. This is what I was looking for. I'm going to experiment a bit with adding a mask variable to the grid datasets
This would also be good to sort out. xarray's nans are just sentinel values. I'm beginning to think there is no reason they should be included in any gridding operation. |
I'm genuinely curious as well. @oehmke is on vacation for a bit. I'll check in with him on this when he gets back. |
I did some tests with ESMPy masking, but could not get any "weight normalization" by using ESMPy mask. The effect of masking seems to be equivalent to setting input data to zero before regridding. For full details please see this gist. I put some key results here. Several cells in the input data are set to Without any masking, With ESMPy masking, the output data get very low values (those near the mask): Such an result is equivalent to setting Did I understand correctly? If so, such a "masking" can be equivalent done by one line of pre-processing code (
It is true that |
|
Just realized that ESMPy masking does make a difference for nearest neighbor algorithm. My above comment still hold for bilinear and conservative methods. Full code available in this slightly modified gist. nearest neighbor + setting nearest neighbor + masking The masked cell are skipped during nearest-neighbor-search, so the values in second-nearest cells are used. Also, the problem of "all weights are nan" does not exist in nearest-neighbor method. If a destination cell is over the ocean (say only land has valid values), a cell along the coast should be found as the nearest cell. I do see the usefulness of this case. Is it possible to avoid the additional |
|
@JiaweiZhuang Nice work on the thorough testing. In the interest of not leading us down the wrong path, I'll work through this with @oehmke when he gets back and present those results. We need to expand the masking docs as well to be more explicit! |
|
@JiaweiZhuang - thanks for doing some extra leg work. I agree we need to hear from the ESMF crew how best to proceed. In the end, I'll be happy if we can fully describe the ESMF behavior, even if #23 isn't merged. |
|
@JiaweiZhuang I've been investigating ESMF masking and have something to run by you. I am using a very simple case for bilinear regridding. There is a 4x4 source grid (squares) with a 3x3 destination grid (star circles) - you'll see these points with the single masked source element in the picture at the end of this post. The coordinates are regional spherical similar to your test grids. The weight file generated with ESMF looks like: You'll notice destination indices |
|
@bekozi Thanks for the example. This agrees with my above results that masking a cell is mathematically equivalent to "setting the input data in that cell to zero" (in bilinear case). One possible advantage of this masking approach (as opposed to zeroing-out the input data) is that it can save some computation by avoiding adding and multiplying on 0s. However, a disadvantage is that two separate regridders need to be built for unmasked and masked input data, even though the underlying grid is the unchanged. The nearest-neighbor method is probably the only case where masking is useful (cannot be replicated by pre&post processing tricks). In your case, I expect that indices
The weight generation in xESMF exactly relies on ESMPy so the behavior is exactly the same. |
|
We've been mostly talking about masking on source cells. On the other hand, masking destination cells seems pretty pointless because it is equivalent to zeroing-out destination cells after regridding. However, destination masking should have some real effect on the "destination to source" nearest-neighbor method, where a masked destination cell should not be able to receive contribution -- according to the principle of I frankly don't know the use case for |
|
Overall, I tend to accept @jhamman's proposal of adding a |
|
Hi, @JiaweiZhuang. If you don't implement masking, then nan values should be left in the field data to ensure the sparse matrix multiplication will create nan values appropriately in the destination field. This assumes your SMM operation containing a nan will return a nan. Setting nan to zero implies data is defined. You will also need to be explicit that "masking" is handled on the field end during SMM by xESMF and degenerate grid coordinates are not supported. For the bilinear test case with the masked element, the weight file is portable as the source grid defines what is masked. Without the mask, the weight file would imply all field data built on that grid is defined at every location. That may be just fine (and preferable) depending on how the weight file is used, but it is something to consider when advising xESMF users on reusing weights. Basically, it comes down to whether you want ESMF or xESMF to determine what is mapped/unmapped following a regridding operation and also if a grid or grid+field is required. |
My bad - I need to be more specific. Degenerate coordinates support through nans will probably work by setting |
|
Thanks both of you for keeping this conversation going. I've been busy working on other things but recently ran into how CDO treats this case. For conservative area remapping, there are two environment variable options that must get passed to the SCRIP library: This seems to cover my personal use case ( |
This is very similar to (probably the same as) #17. But this normalization would not help if a destination cell has no overlap with unmasked source cells (i.e. all overlapping source cells are masked). You can still get some |
@bekozi thanks for the notice! How is "degenerate coordinates" exactly defined here? My understanding of a "degenerated grid cell" is when two corner points coincide and the cell becomes a triangle. But do you simply mean "masking" here? |
|
Hi @JiaweiZhuang, you are partially correct about what an ESMF considers a degenerate cell. Instead of two points collapsing to leave a triangle, for ESMF a degenerate cell is one where enough points collapse to leave a cell either a line or a point. Regarding the earlier question about fracarea, in ESMF we don't divide if the destination fraction is 0.0, so we don't get nans. (I think that was what you were asking (?)) |
|
@jhamman Just a quick note: the "re-normalization" you need can be enabled by applying masks and setting One use case for this is to regrid emission data that is only defined over the land. With This only works for conservative algorithm. There is no "re-normalization" for bilinear algorithm, where masking literally means zeroing nans. |
|
Thanks @JiaweiZhuang - this is exactly what I was going for. |
|
@JiaweiZhuang - circling back here. What do you think the next steps should be to resolve this issue. Your example above is compelling to the point I would like to see some explicit support for this use case in xESMF. |
|
@jhamman It is in the regridder = xe.Regridder(grid_in, grid_out, method='conservative_normed')where |
|
@JiaweiZhuang, just to clarify |
|
@NicWayand |
|
Ah yes, thank you. |
|
Thanks for this package. It would be great to have @jhamman pull requests merged into master. Please let me know if there is anything I can do for help. |
Co-authored-by: Anderson Banihirwe <[email protected]>
|
For a more recent discussion on this topic, see pangeo-data/xESMF#256 |
|
Closing in favor of the issue above. |







I have a use case where I am regridding from/to grids that have missing values in them (water mask over land). I'm curious how xESMF is treating these grid cells. I am noticing a large difference in how the grids come out between the bilinear and conservative regridding methods. For example:
bilinear:
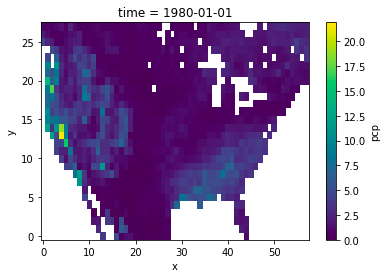
conservative:
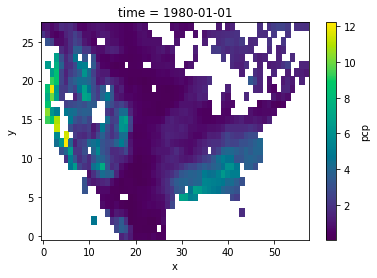
I should note, this regridding operation is a coarse-graining operation so there are up to 64 1/8th deg source grid cells going into each 1 deg dest grid cell.
The text was updated successfully, but these errors were encountered: