GUIDE.md

Bend in X minutes - the ultimate guide!

Bend is a high-level, massively parallel programming language. That means it feels like Python, but scales like CUDA. It runs on CPUs and GPUs, and you don't have to do anything to make it parallel: as long as your code isn't "helplessly sequential", it will use 1000's of threads!

While cool, Bend is far from perfect. In absolute terms it is still not so fast. Compared to SOTA compilers like GCC or GHC, our code gen is still embarrassingly bad, and there is a lot to improve. And, of course, in this beginning, there will be tons of instability and bugs. That said, it does what it promises: scaling horizontally with cores. And that's really cool! If you'd like to be an early adopter of this interesting tech, this guide will teach you how to apply Bend to build parallel programs in a new way!

For a more technical dive, check HVM2's paper. For an entertaining, intuitive explanation, see HVM1's classic HOW.md. But if you just want to dive straight into action - this guide is for you. Let's go!

Installation

Install dependencies

On Linux

# Install Rust if you haven't it already.
curl --proto '=https' --tlsv1.2 -sSf https://sh.rustup.rs | sh

# For the C version of Bend, use GCC. We recommend a version up to 12.x.
sudo apt install gcc

For the CUDA runtime install the CUDA toolkit for Linux version 12.x.

On Mac

# Install Rust if you haven't it already.
curl --proto '=https' --tlsv1.2 -sSf https://sh.rustup.rs | sh

# For the C version of Bend, use GCC. We recommend a version up to 12.x.
brew install gcc

Install Bend

1. Install HVM2 by running:

# HVM2 is HOC's massively parallel Interaction Combinator evaluator.
cargo install hvm

# This ensures HVM is correctly installed and accessible.
hvm --version

2. Install Bend by running:

# This command will install Bend
cargo install bend-lang

# This ensures Bend is correctly installed and accessible.
bend --version

Hello, World!

As we said, Bend feels like Python - in some ways. It is high-level, you can easily create objects and lists, there are ifs and loops. Yet, it is different: there is some Haskell in it, in the sense algebraic datatypes, pattern-matching and recursion play an important role. This is how its "Hello, world!" looks:

def main():
  return "Hello, world!"

Wait - there is something strange there. Why return, not print? Well, for now (you'll read these words a lot), Bend doesn't have IO. We plan on introducing it very soon! So, for now, all you can do is perform computations, and see results. To run the program above, type:

bend run-rs main.bend

If all goes well, you should see "Hello, world!". The bend run-rs command uses the reference interpreter, which is slow. In a few moments, we'll teach you how to run your code in parallel, on both CPUs and GPUs. For now, let's learn some fundamentals!

Basic Functions and Datatypes

In Bend, functions are pure: they receive something, and they return something. That's all. Here is a function that tells you how old you are:

def am_i_old(age):
  if age < 18:
    return "you're a kid"
  else:
    return "you're an adult"

def main():
  return am_i_old(32)

That is simple enough, isn't it? Here is one that returns the distance between two points:

def distance(ax, ay, bx, by):
  dx = bx - ax
  dy = by - ay
  return (dx * dx + dy * dy) ** 0.5

def main():
  return distance(10.0, 10.0, 20.0, 20.0)

This isn't so pretty. Could we use tuples instead? Yes:

def distance(a, b):
  (ax, ay) = a
  (bx, by) = b
  dx = bx - ax
  dy = by - ay
  return (dx * dx + dy * dy) ** 0.5

def main():
  return distance((10.0, 10.0), (20.0, 20.0))

So far, this does look like Python, doesn't it? What about objects? Well - here, there is a difference. In Python, we have classes. In Bend, we just have the objects themselves. This is how we create a 2D vector:

object V2 { x, y }

def distance(a, b):
  open V2: a
  open V2: b
  dx = b.x - a.x
  dy = b.y - a.y
  return (dx * dx + dy * dy) ** 0.5

def main():
  return distance(V2 { x: 10.0, y: 10.0 }, V2 { x: 20.0, y: 20.0 })

This doesn't look too different, does it? What is that open thing, though? It just tells Bend to consume the vector, a, "splitting" it into its components, a.x and a.y. Is that really necessary? Actually, no - not really. But, for now, it is. This has to do with the fact Bend is an affine language, which... well, let's not get into that. For now, just remember we need open to access fields.

Bend comes with 3 built-in numeric types: u24, i24, f24. That's quite small, we admit. Soon, we'll have larger types. For now, that's what we got. The u24 type is written like 123 or 0xF. The i24 type requires a sign, as in, +7 or -7. The f24 type uses ., like 3.14.

Other than tuples, Bend has another, very general, way to encode data: datatypes! These are just "objects with tags". A classic example of this is a "shape", which can be either a circle or a rectangle. It is defined like this:

type Shape:
  Circle { radius }
  Rectangle { width, height }

def area(shape):
  match shape:
    case Shape/Circle:
      return 3.14 * shape.radius ** 2.0
    case Shape/Rectangle:
      return shape.width * shape.height

def main:
  return area(Shape/Circle { radius: 10.0 })

In this example, Shape is a datatype with two variants: Circle and Rectangle. The area function uses pattern matching to handle each variant appropriately. Just like objects need open, datatypes need match, which give us access to fields in each respective case.

Datatypes are very general. From matrices, to JSON, to quadtrees, every type of data can be represented as a datatype (I mean, that's the name!). In fact, lists - which, on Python, are actually stored as arrays - are represented using datatypes on Bend. Specifically, the type:

type List:
  Nil
  Cons { head, ~tail }

Here, the Nil variant represents an empty list, and the Cons variant represents a concatenation between an element (head) and another list (tail). That way, the [1,2,3] list could be written as:

def main:
  my_list = List/Cons { head: 1, tail: List/Cons { head: 2, tail: List/Cons { head: 3, tail: List/Nil }}}
  return my_list

Obviously - that's terrible. So, you can write just instead:

def main:
  my_list = [1, 2, 3]
  return my_list

Which is decent. But while it is written the same as in Python, it is important to understand it is just the List datatype, which means we can operate on it using the match notation. For example:

def main:
  my_list = [1, 2, 3]
  match my_list:
    case List/Cons:
      return my_list.head
    case List/Nil:
      return 0

Will return 1, which is the first element.

NOTE: Despite creating lists with [ ], the syntax used for accessing values as in type[key] is actually related to the Map built-in type.

We also have a syntax sugar for strings in Bend, which is just a list of u24 characters (UTF-16 encoded). The "Hello, world!" type we've seen used it!

NOTE: The actual type used for strings is String, which has String/Cons and String/Nil just like List does.

Bend also has inline functions, which work just like Python:

def main:
  mul_2 = lambda x: x * 2
  return mul_2(7)

Except without the annoying syntax restrictions. You can also shorten it as λ, if you can somehow type that.

You can also match on native numbers (u24) using the switch statement:

def slow_mul2(n):
  switch n:
    case 0:
      return 0
    case _:
      return 2 + slow_mul2(n-1)

The if-else syntax is a third option to branch, other than match and switch. It expects a u24 (1 for true and 0 for false):

def is_even(n):
  if n % 2 == 0:
    return 1
  else:
    return 0

note - some types, like tuples, aren't being pretty-printed correctly after computation. this will be fixed in the next days (TM)

The Dreaded Immutability

Finally, let's get straight to the fun part: how do we implement parallel algorithms with Bend? Just kidding. Before we get there, let's talk about loops. You might have noticed we have avoided them so far. That wasn't by accident. There is an important aspect on which Bend diverges from Python, and aligns with Haskell: variables are immutable. Not "by default". They just are. For example, in Bend, we're not allowed to write:

def parity(x):
  result = "odd"
  if x % 2 == 0:
    result = "even"
  return result

... because that would mutate the result variable. Instead, we should write:

def is_even(x):
  if x % 2 == 0:
    return "even"
  else:
    return "odd"

def main:
  return is_even(7)

Which is immutable. If that sounds annoying, that's because it is. Don't let anyone tell you otherwise. We are aware of that, and we have many ideas on how to improve this, making Bend feel even more Python-like. For now, we have to live with it. But, wait... if variables are immutable... how do we even do loops? For example:

def sum(x):
  total = 0
  for i in range(10)
    total += i
  return total

Here, the entire way the algorithm works is by mutating the total variable. Without mutability, loops don't make sense. The good news is Bend has something else that is equally as - actually, more - powerful. And learning it is really worth your time. Let's do it!

Folds and Bends

Recursive Datatypes

Let's start by implementing a recursive datatype in Bend:

type Tree:
  Node { ~left, ~right }
  Leaf { value }

This defines a binary tree, with elements on leaves. Here, ~ flags a field as recursive. For example, the tree:

  __/\__
 /\     /\
1  2   3  4

Could be represented as:

tree = Tree/Node {
  lft: Tree/Node { left: Tree/Leaf { val: 1 }, right: Tree/Leaf { val: 2 } },
  rgt: Tree/Node { left: Tree/Leaf { val: 3 }, right: Tree/Leaf { val: 4 } }
}

Binary trees are so useful in Bend that this type is already pre-defined in the language and has its own dedicated syntax:

# ![a, b] => Equivalent to Tree/Node { left: a, right: b }
# !x      => Equivalent to Tree/Leaf { value: x }
tree = ![![!1, !2],![!3, !4]]

Fold: consuming recursive datatypes

Now, here's a question: how do we sum the elements of a tree? In Python, we could just use a loop. In Bend, we don't have loops. Fortunately, there is another construct we can use: it's called fold, and it works like a search and replace for datatypes. For example, consider the code below:

def sum(tree):
  fold tree:
    case Tree/Node:
      return tree.left + tree.right
    case Tree/Leaf:
      return tree.value

def main:
  tree = ![![!1, !2],![!3, !4]]
  return sum(tree)

It accomplishes the task by replacing every Tree/Node { left, right } by left + right, and replacing every Tree/Leaf by value. As a result, the entire "tree of values" is turned into a "tree of additions", and it evaluates as follows:

nums = ((1 + 2) + (3 + 4))
nums = (3 + 7)
nums = 10

Now, this may look limiting, but it actually isn't. Folds are known for being universal: any algorithm that can be implemented with a loop, can be implemented with a fold. So, we can do much more than just compute an "aggregated value". Suppose we wanted, for example, to transform every element into a tuple of (index,value), returning a new tree. Here's how to do it:

def enum(tree):
  idx = 0
  fold tree with idx:
    case Tree/Node:
      return ![tree.left(idx * 2 + 0), tree.right(idx * 2 + 1)]
    case Tree/Leaf:
      return !(idx, tree.value)

def main:
  tree = ![![!1, !2],![!3, !4]]
  return enum(tree)

Compared to the sum algorithm, 3 important things changed:

1. We initialize a state, idx, as 0.

2. We pass new states down as tree.xyz(new_idx)

3. The base case receives the final state: the element index

So, in the end, we'll have computed a copy of the original tree, except that every element has now became a tuple of index and value.

Now, please take a moment to think about this fact: everything can be computed with a fold. This idea often takes some time to get used to, but, once you do, it is really liberating, and will let you write better algorithms. As an exercise, use fold to implement a "reverse" algorithm for lists:

def reverse(list):
  # exercise
  ?

def main:
  return reverse([1,2,3])

Bend: generating recursive datatypes

Bending is the opposite of folding. Whatever fold consumes, bend creates. The idea is that, by defining an initial state and a halting condition, we can "grow" a recursive structure, layer by layer, until the condition is met. For example, consider the code below:

def main():
  bend x = 0:
    when x < 3:
      tree = ![fork(x + 1), fork(x + 1)]
    else:
      tree = !7
  return tree

The program above will initialize a state (x = 0), and then, for as long as x < 3, it will "fork" that state in two, creating a Tree/Node, and continuing with x + 1. When x >= 3, it will halt and return a Tree/Leaf with 7. When all is done, the result will be assigned to the tree variable:

tree = fork(0)
tree = ![fork(1), fork(1)]
tree = ![![fork(2),fork(2)], ![fork(2),fork(2)]]
tree = ![![![fork(3),fork(3)], ![fork(3),fork(3)]], ![![fork(3),fork(3)], ![fork(3),fork(3)]]]
tree = ![![![!7, !7], ![!7, !7]], ![![!7, !7], ![!7, !7]]]

With some imagination, we can easily see that, by recursively unrolling a state this way, we can generate any structure we'd like. In fact, bend is so general we can even use it to emulate a loop. For example, this Python program:

sum = 0
idx = 0
while idx < 10:
  sum = idx + sum
  idx = idx + 1

Could be emulated in Bend with a "sequential bend":

bend idx = 0:
  when idx < 10:
    sum = idx + fork(idx + 1)
  else:
    sum = 0

Of course, if you do it, Bend's devs will be very disappointed with you. Why? Because everyone is here for one thing. Let's do it!

Parallel "Hello, World"

So, after all this learning, we're now ready to answer the ultimate question:

How do we write parallel algorithms in Bend?

At this point, you might have the idea: by using folds and bends, right? Well... actually not! You do not need to use these constructs at all to make it happen. Anything that can be parallelized will be parallelized on Bend. To be more precise, this:

f(g(x))

Can NOT be parallelized, because f depends on the result of g. But this:

H(f(x), g(y))

Can be parallelized, because f(x) and g(y) are independent. Traditional loops, on the other hands, are inherently sequential. A loop like:

sum = 0
for i in range(8):
  sum += i

Is actually just a similar way to write:

sum = (0 + (1 + (2 + (3 + (4 + (5 + (6 + 7)))))))

Which is really bad for parallelism, because the only way to compute this is by evaluating the expressions one after the other, in order:

sum = (0 + (1 + (2 + (3 + (4 + (5 + (6 + 7)))))))
sum = (0 + (1 + (2 + (3 + (4 + (5 + 13))))))
sum = (0 + (1 + (2 + (3 + (4 + 18)))))
sum = (0 + (1 + (2 + (3 + 22))))
sum = (0 + (1 + (2 + 25)))
sum = (0 + (1 + 27))
sum = (0 + 28)
sum = 28

There is nothing Bend could do to save this program: sequentialism is an inherent part of its logic. Now, if we had written, instead:

sum = (((0 + 1) + (2 + 3)) + ((4 + 5) + (6 + 7)))

Then, we'd have a much easier time evaluating that in parallel. Look at it:

sum = (((0 + 1) + (2 + 3)) + ((4 + 5) + (6 + 7)))
sum = ((1 + 5) + (9 + 13))
sum = (6 + 22)
sum = 28

That's so much better that even the line count is shorter!

So, how do you write a parallel program in Bend?

Just write algorithms that aren't helplessly sequential.

That's all there is to it. As long as you write programs like that one, then unlike the former one, they will run in parallel. And that's why bend and fold are core features: they're, essentially, parallelizable loops. For example, to add numbers in parallel, we can write:

def main():
  bend d = 0, i = 0:
    when d < 28:
      sum = fork(d+1, i*2+0) + fork(d+1, i*2+1)
    else:
      sum = i
  return sum

And that's the parallel "Hello, world"! Now, let's finally run it. But first, let's measure its single-core performance. Also, remember that, for now, Bend only supports 24-bit numbers (u24), thus, the results will always be in mod 16777216.

bend run-rs main.bend

On my machine (Apple M3 Max), it completes after 147s, at 65 MIPS (Million Interactions Per Second - Bend's version of the FLOPS). That's too long. Let's run it in parallel, by using the C interpreter instead:

bend run main.bend

Note: run is an alias to the run-c command.

And, just like that, the same program now runs in 8.49s, at 1137 MIPS. That's 18x faster! Can we do better? Sure: let's use the C compiler now:

bend gen-c main.bend >> main.c

This command converts your bend file into a small, dependency-free C file that does the same computation much faster. You can compile it to an executable:

gcc main.c -o main -O2 -lm -lpthread # if you're on Linux
gcc main.c -o main -O2               # if you're on OSX
./main

Now, the same program runs in 5.81s, at 1661.91 MIPS. That's now 25x faster than the original! Can we do better? Let's now enter the unexplored realms of arbitrary high-level programs on... GPUs. How hard that could be? Well, for us... it was. A lot. For you... just call the CUDA interpreter:

bend run-cu main.bend

And, simply as that, the same program now runs in 0.82s, at a blistering 11803.24 MIPS. That's 181x faster than the original. Congratulations! You're now a thread bender.

~

As a last note, you may have noticed that the compiled version isn't much faster than the interpreted one. Our compiler is still on its infancy, and the assembly generated is quite abysmal. Most of our effort went into setting up a foundation for the parallel evaluator, which was no easy task. With that out of our way, improving the compiler is a higher priority now. You can expect it to improve continuously over time. For now, it is important to understand the state of things, and set up reasonable expectations.

A Parallel Bitonic Sort

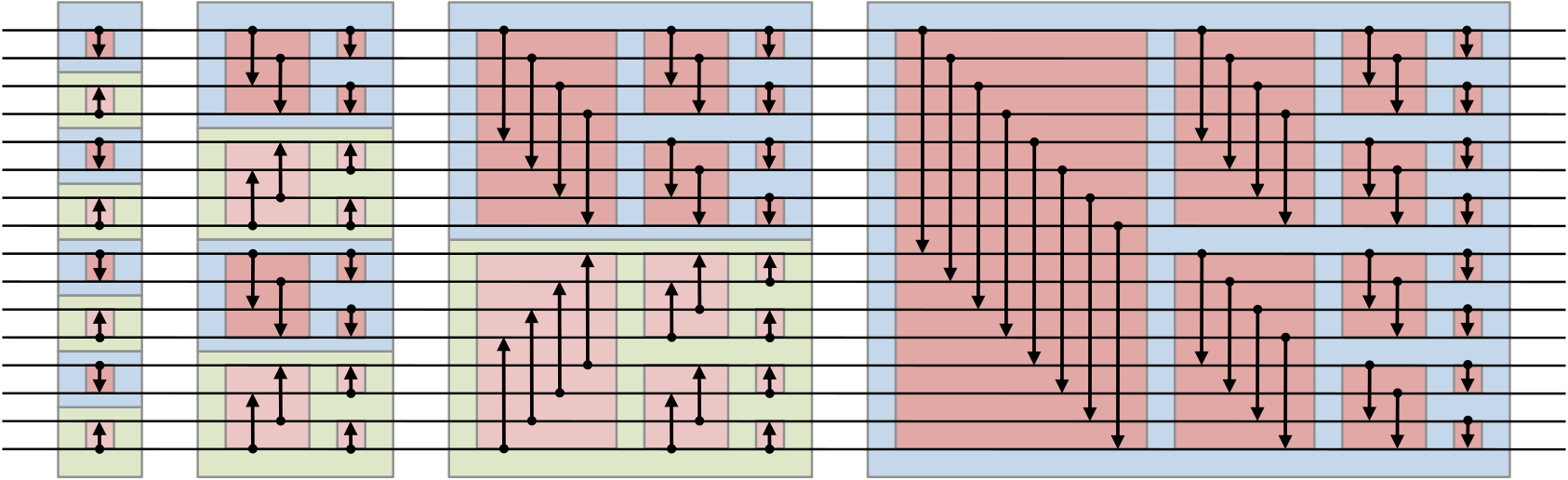
The bitonic sort is a popular algorithm that sorts a set of numbers by moving them through a "circuit" (sorting network) and swapping as they pass through:

In CUDA, this can be implemented by using mutable arrays and synchronization primitives. This is well known. What is less known is that it can also be implemented as a series of immutable tree rotations, with pattern-matching and recursion. Don't bother trying to understand it, but, here's the code:

def gen(d, x):
  switch d:
    case 0:
      return x
    case _:
      return (gen(d-1, x * 2 + 1), gen(d-1, x * 2))

def sum(d, t):
  switch d:
    case 0:
      return t
    case _:
      (t.a, t.b) = t
      return sum(d-1, t.a) + sum(d-1, t.b)

def swap(s, a, b):
  switch s:
    case 0:
      return (a,b)
    case _:
      return (b,a)

def warp(d, s, a, b):
  switch d:
    case 0:
      return swap(s ^ (a > b), a, b)
    case _:
      (a.a,a.b) = a
      (b.a,b.b) = b
      (A.a,A.b) = warp(d-1, s, a.a, b.a)
      (B.a,B.b) = warp(d-1, s, a.b, b.b)
      return ((A.a,B.a),(A.b,B.b))

def flow(d, s, t):
  switch d:
    case 0:
      return t
    case _:
      (t.a, t.b) = t
      return down(d, s, warp(d-1, s, t.a, t.b))

def down(d,s,t):
  switch d:
    case 0:
      return t
    case _:
      (t.a, t.b) = t
      return (flow(d-1, s, t.a), flow(d-1, s, t.b))

def sort(d, s, t):
  switch d:
    case 0:
      return t
    case _:
      (t.a, t.b) = t
      return flow(d, s, (sort(d-1, 0, t.a), sort(d-1, 1, t.b)))

def main:
  return sum(18, sort(18, 0, gen(18, 0)))

As a test of Bend's ability to parallelize the most insanely high-level computations possible, let's benchmark this program. Here are the results:

• 12.33s / 102 MIPS (Apple M3 Max, 1 thread)

• 0.96s / 1315 MIPS (Apple M3 Max, 16 threads) - 12x speedup

• 0.24s / 5334 MIPS (NVIDIA RTX 4090, 16k threads) - 51x speedup

And, just like magic, it works! 51x faster on RTX. How cool is that?

Of course, you would absolutely not want to sort numbers like that, specially when mutable arrays exist. But there are many algorithms that can not be implemented easily with buffers. Evolutionary and genetic algorithms, proof checkers, compilers, interpreters. For the first time ever, you can implement these algorithms as high-level functions, in a language that runs on GPUs. That's the magic of Bend!

Graphics Rendering

While the algorithm above does parallelize well, it is very memory-hungry. It is a nice demo of Bend's potential, but isn't a great way to sort lists. Currently, Bend has a 4GB memory limit (for being a 32-bit architecture). When the memory is filled, its performance will degrade considerably. But we can do better.

Since Bend is GC-free, we can express low memory footprint programs using bend or tail calls. For maximum possible performance, one should first create enough "parallel room" to fill all available cores, and then spend some time doing compute-heavy, but less memory-hungry, computations. For example, consider:

# given a shader, returns a square image
def render(depth):
  bend d = 0, i = 0:
    when d < depth:
      color = (fork(d+1, i*2+0), fork(d+1, i*2+1))
    else:
      width = depth / 2
      color = demo_shader(i % width, i / width)
  return color

# given a position, returns a color
# for this demo, it just busy loops
def demo_shader(x, y):
  bend i = 0:
    when i < 100000:
      color = fork(i + 1)
    else:
      color = 0x000001
  return color

# renders a 256x256 image using demo_shader
def main:
  return render(16, demo_shader)

It emulates an OpenGL fragment shader by building an "image" as a perfect binary tree, and then calling the demo_shader function on each pixel. Since the tree has a depth of 16, we have 2^16 = 65536 pixels, which is enough to fill all cores of an RTX 4090. Moreover, since demo_shader isn't doing many allocations, it can operate entirely inside the GPU's "shared memory" (L1 cache). Each GPU thread has a local space of 64 IC nodes. Functions that don't need more than that, like demo_shader, can run up to 5x faster!

On my GPU, it performs 22,000 MIPS out of the box, and 40000+ MIPS with a tweak on the generated CUDA file (doubling the TPC, which doubles the number of threads per block). In the near future, we plan to add immutable textures, allowing for single-interaction sampling. With some napkin math, this should be enough to render 3D games in real-time. Imagine a future where game engines are written in Python-like languages? That's the future we're building, with Bend!

You can see your programs total cost (number of interactions) and performance (MIPS) by adding the -s flag. This is a good way to check if your algorithm is parallelizing. For example, on my Apple M3 Max, sequential algorithms will perform about 100 MIPS on interpreted mode, and 130 MIPS on compiled mode (remember our compiler is still very immature, which is why it isn't much faster than the interpreter). A well-parallelizable program, though, will easily reach 1000+ MIPS.

To be continued...

This guide isn't extensive, and there's a lot uncovered. For example, Bend also has an entire "secret" Haskell-like syntax that is compatible with old HVM1. Here is an implementation of the Bitonic Sort with Haskell-like equations. We'll document its syntax here soon!

Community

Remember: Bend is very new and experimental. Bugs and imperfections should be expected. That said, HOC will provide long-term support to Bend (and its runtime, HVM2). So, if you believe this paradigm will be big someday, and want to be part of it in these early stages, join us on Discord. Report bugs, bring your suggestions, and let's chat and build this future together!